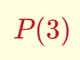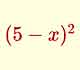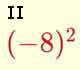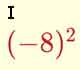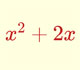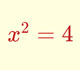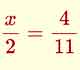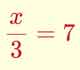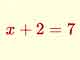|
|
17 de enero de 2025
Mecanismos articulados y Matemáticas
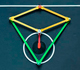 |
Presentación de algunos mecanismos articulados y su relación con las Matemáticas. Modelos realizados con materiales sencillos, impresión 3D. Algunos modelos motorizados y controlados con Arduino.
|
30 de Mayo de 2022
Los sólidos arquimedianos
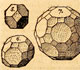 |
Exposición sobre los sólidos arquimedianos realizados por alumnos de 1ºESO del IES Alonso Quijano de Alcalá de Henares.
|
9 de Mayo de 2022
Diez tetraedros en un dodecaedro
 |
Se pueden colocar cinco tetraedros en un dodecaedro de dos formas distintas, quirales. La combinación de estos dos poliedros da lugar al compuesto de diez tetraedros en un dodecaedro.
|
28 de Febrero de 2022
Tetraxis
 |
Tetraxis es un puzle muy interesante, sencillo y bonito, diseñado por Jane y John Kostick. Estudiaremos algunas propiedades de este juego y su relación con el dodecaedro rómbico. Plantillas para construir un Tetraxis con cartulina e imanes. El rompecabezas hecho con impresión 3D.
|
13 de Septiembre de 2021
Cinco tetraedros
 |
Construcción de cinco tetraedros en un dodecaedro con diferentes técnicas: cartulina, origami, tubos, tensegrity. Justificación de esta preciosa construcción.
|
24 de Mayo de 2021
Poliedros platónicos
 |
Exposición sobre los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro. Construcción de los poliedros encajados. El Omnipoliedro. Algunas propiedades básicas que se pueden aprender de esta construcción.
|
19 de Octubre de 2020
Cálculo mental básico
 |
Aplicación para practicar cálculo mental con raíces cuadradas, producto de raíces y extracción de factores.
|
 |
Aplicación para practicar cálculo mental con decimales multiplicados o divididos por potencias de 10: por diez, por cien, por mil, por una décima, una centésima o una milésisma.
|
28 de Septiembre de 2020
Cálculo mental básico
 |
Aplicación para practicar el cálculo mental del m.c.d y del m.c.m de dos números.
|
1 de Junio de 2020
Despedida del proyecto 'matemáticasVisuales En casa': el enanito que desaparece
 |
Conocido rompecabezas en el que al cambiar dos piezas de un dibujo desaparece uno de los enanitos. ¿Qué explicación tiene?.
|
27 de Mayo de 2020
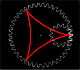 |
Generación mediante engranajes de varias curvas de la familia de las hipocicloides: astroide, deltoide y otras.
|
 |
Más ejemplos de curvas de la familia de las hipocicloides generadas mediante engranajes.
|
 |
Generación mediante engranajes de varias curvas de la familia de las epicicloides: cardiode, nefroide y otras.
|
25 de Mayo de 2020
Cicloide y epicicloides
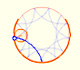 |
Se presenta la cicloide y se muestra una deformación continua de la cicloide en otras hipocicloides como la deltoide.
|
22 de Mayo de 2020
 |
Las torres de Hanoi es un rompecabezas que aquí se presenta haciendo una versión sobre un cuadro de Magritte.
|
20 de Mayo de 2020
Volumen del tetraedro
 |
Construcción con pajitas de refresco de un octaedro al que se le añaden cuatro tetraedros para obtener un tetraedro grande.
|
 |
Añadiendo cuatro tetraedros a un octaedro podemos obtener un tetraedro. Calculamos el volumen de un tetraedro a partir del volumen de un octaedro y usando semejanza.
|
18 de Mayo de 2020
Un tetraedro en un cubo
 |
Una manera muy elegante de dar rigidez al cubo es construir un tetraedro dentro del cubo. A partir de un cubo se pueden construir dos tetradros distintos de este modo.
|
 |
Estudiamos algunas medidas de la construcción de un tetraedro en un cubo. Calculamos el volumen del cubo a partir de la arista del tetraedro.
|
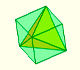 |
Podemos inscribir un tetraedro en un cubo. A partir de esta construcción calculamos el volumen de un tetraedro.
|
15 de Mayo de 2020
Circunferencias
 |
Animación inspirada en el trabajo de Jean Louis Nicolet y Caleb Gattegno sobre circunferencias que pasan por dos puntos.
|
 |
Animación inspirada en el trabajo de Jean Louis Nicolet y Caleb Gattegno sobre circunferencias que pasan por tres puntos.
|
13 de Mayo de 2020
Circunferencias y círculos
 |
Todas las circunferencias son semejantes. Esta idea tan simple nos lleva a un concepto muy importante, la definición del número Pi.
|
 |
Una aproximación intuitiva al área de un círculo. Para calcular el área de un círculo también necesitamos el número Pi.
|
11 de Mayo de 2020
Origami para los más pequeños
 |
Plegado y decoración de una piraña de origami. Figura muy sencilla para introducir a los más pequeños en el origami. A un paso de hacer la pajarita.
|
8 de Mayo de 2020
Rectángulos áureos
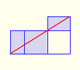 |
Los rectángulos áureos están relacionados con los pentágonos regulares. Exploramos alguna propiedad de estos rectángulos.
|
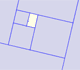 |
La propiedad de los rectángulos áureos nos lleva a un interesante proceso infinito.
|
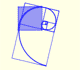 |
Partiendo de un rectángulo áureo podemos dibujar la preciosa y sencilla espiral de Durero.
|
6 de Mayo de 2020
Rectángulos
 |
No todos los rectángulos son semejantes pues tienen distintas formas, unos son más alargados que otros.
|
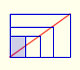 |
El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.
|
 |
Calculamos la relación entre el largo y el ancho de una hoja de papel Din A4.
|
5 de Mayo de 2020
Más ejercicios sobre áreas y volúmenes
 |
Construcción de una piscina de cartulina a escala. Haremos algunos cálculos a partir de esa construcción.
|
 |
Ejercicio sobre el volumen y peso de la cabeza de un martillo.
|
4 de Mayo de 2020
Origami modular
 |
Plegado de un tetraedro usando dos módulos de origami. Se propone la construcción de un cubo de cartulina en el que cabe nuestro tetraedro.
|
3 de Mayo de 2020
Datos de visitas a matemáticasVisuales
 |
La representación gráfica de datos nos muestra los datos de un modo visual e intuitivo. Se muestran ejemplos en relación con el estudiio de las visitas al sitio matemátivasVisuales.
|
2 de Mayo de 2020
El pentágono
 |
La diagonal y el lado de un pentágono regular están en proporción áurea. Utilizando semejanza llegaremos a calcular el valor de la razón áurea.
|
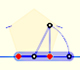 |
Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.
|
28 de Abril de 2020
Funciones racionales
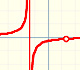 |
Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.
|
 |
Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.
|
27 de Abril de 2020
Ángulos
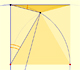 |
Se propone una construcción con regla y compás y probar la medida de un ángulo del dibujo.
|
26 de Abril de 2020
Magia
 |
Propuesta de dibujar unas tarjetas para hacer un truco de magia apto para los más jóvenes. Con ellas adivinaremos el pensamiento. El fundamento matemático es muy interesasnte.
|
25 de Abril de 2020
Ángulos
 |
Si doblamos un cuadrado de papel por la mitad obtenemos un triángulo. ¿Qué ángulos se han formado? ¿Cómo es el triángulo?.
|
 |
Con unos sencillos pliegues podemos doblar un triángulo equilátero. ¿Sabrías demostrar que los ángulos son de 30º y de 60º?.
|
23 de Abril de 2020
Funciones polinómicas que dependen de un parámetro
 |
Representación de una familia de funciones afines que dependen de un parámetro.
|
21 de Abril de 2020
Más ejercicios de la Primavera Matemática de nivel 1
 |
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
|
20 de Abril de 2020
 |
Técnica sencilla para construir poliedros pegando discos de cartulina o de cartón de caja de galletas. Se propone la construcción de un icosaedro.
|
18 de Abril de 2020
Análisis. Continuidad de funciones
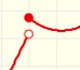 |
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Las dos funciones que definen los trozos son afines.
|
 |
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Discontinuides de salto. Las dos funciones que definen los trozos son afines.
|
 |
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Discontinuides de salto. Las dos funciones que definen los trozos son afines.
|
 |
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Discontinuides de salto. Las dos funciones que definen los trozos son afines.
|
 |
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Discontinuides de salto. Una de las funciones es afín y la otra es quadrática.
|
 |
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Discontinuides de salto. Una de las funciones es afín y la otra es quadrática.
|
17 de Abril de 2020
 |
Dibujo del desarrollo de una casita a escala. Haremos algunos cálculos a partir de esa construcción.
|
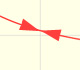 |
Estudio del concepto de continuidad de una función desde un punto de vista intuitivo. Algunos tipos de discontinuidades.
|
16 de Abril de 2020
 |
Proponemos hacer esta famosa construcción del esqueleto de un icosaedro formado por tres rectángulos áureos usando el cartón de una caja de leche.
|
15 de Abril de 2020
 |
Podemos construir un cuadrado doblando y cortando un folio. Se trata de un ejercicio muy básico de origami. Mediremos la diagonal.
|
 |
Podemos construir un cuadrado con pajitas de refresco. Notamos que no es rígido. Si lo deformamos obtenemos rombos. Para conseguir que sea rígido podemos añadir una pajita en la diagonal.
|
14 de Abril de 2020
Homenaje a John Conway: el Juego de la Vida
 |
El Juego de la Vida, inventado por John H. Conway, es uno de los autómatas celulares bidimensionales más famosos.
|
13 de Abril de 2020
 |
Construcción de una sección rómbica del cubo con pajitas de refresco. Hacemos unos cálculos sobre esa sección.
|
11 de Abril de 2020
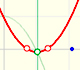 |
Estudio y clasificación de una familia polinómica de grado 2 que depende de un parámetro. Sus dos raíces pueden ser las dos reales y distintas, una raíz real doble o dos raíces complejas conjugadas.
|
 |
Estudio de las raíces reales o complejas de una familia polinómica de grado 2 que depende de un parámetro. Representación gráfica en el plano complejo.
|
8 de Abril de 2020
 |
Actividad de origami tradicional, muy sencilla de hacer y muy bonita. Nos introduce en el conocimiento del pentágono y sus diagonales.
|
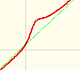 |
Para valores grandes en valor absoluto de la variable x algunas funciones se comportan como una recta oblicua. A esta recta la llamamos asíntota oblicua de la función.
|
7 de Abril de 2020
 |
Vamos a calcular la diagonal de un cuadrado. Para presentar la idea usaremos el lenguaje de las funciones.
|
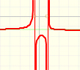 |
Si el denominador de una función racional es un polinomio de grado 2 la función tiene dos, una o ninguna singularidad real (asíntotas verticales y singularidades evitables).
|
6 de Abril de 2020
Nueva sección de En casa: Actualizaciones
 |
En casa se actualiza, por lo menos, 5 veces a la semana mientras dura el confinamiento. Aquí se puede ver la sucesión cronológica de las publicaciones.
|
 |
Todos los cuadrados son semejantes. Estudiamos la relación entre lado y diagonal de un modo intuitivo.
|
 |
Todos los cuadrados son semejantes. Estudiamos la relación entre lado y diagonal usando el lenguaje de las funciones.
|
 |
Si colocamos una diagonal en nuestro cuadrado conseguimos darle rigidez. Calculamos la diagonal usando el teorema de Pitágoras.
|
3 de Abril de 2020
Nueva sección de En casa: cálculo mental
 |
Ejercicios de cálculo mental en el que se practican algunas estructuras básicas con el propósito de mejorar la seguridad y autoconfianza.
|
 |
Construcción de un tetraedro con un rollo de papel higiénico. Esta técnica se usó y todavía se usa para envasar productos.
|
2 de Abril de 2020
 |
Construcción de los cinco sólidos platónicos con pajitas de refresco. Contamos sus elementos (sus caras, aristas y vértices) y vemos si son rígidos o no.
|
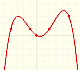 |
Se trata de encontrar el polinomio de menor grado que pasa por una serie de puntos del plano. Es un problema de interpolación que aquí resolvemos usando los polinomios de Lagrange.
|
 |
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
|
1 de Abril de 2020
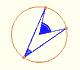 |
Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.
|
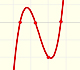 |
Las funciones cúbicas son polinomios de grado 3. Una función cúbica real siempre corta al eje de abcisas por lo menos una vez.
|
 |
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
|
31 de Marzo de 2020
 |
Estudiamos el concepto de dualidad de poliedros aplicado a los sólidos platónicos. El cubo y el octaedro son duales, el icosaedro y el dodecaedro son duales y el tetraedro decimos que es autodual.
|
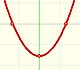 |
Las funciones cuadráticas son polinomios de grado 2. Sus gráficas son parábolas. Para encontrar los puntos de corte con el eje de abcisas tenemos que resolver una ecuación. El vértice de la parábola es un máximo o mínimo de la función.
|
 |
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
|
30 de Marzo de 2020
Se inicia la publicación de matemáticasVisuales.En casa
 |
Página con enlaces de actividades matemáticas que podemos hacer en casa.
|
 |
Página con enlaces de actividades matemáticas fáciles que podemos hacer en casa. Pensadas para alumnos de Educación Secundaria, edad aproximada 12-16 años.
|
 |
Página con enlaces de actividades matemáticas que podemos hacer en casa un poco más complicadas. Pensadas para alumnos de Bachillerato o último año de Educación Secundaria. Edad aproximada, a partir de 15 años.
|
 |
Si tenemos impresora en casa podemos imprimir plantillas en cartulina (o papel) y hacer interesantes construcciones. Muchas son sencillas y puedes intentar hacerlas con reglas y compás. Aunque no puedas hacerlas, también puedes mirarlas pues de ellas sacaremos interesantes consecuencias matemáticas.
|
 |
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
|
 |
Construcción de un octaedro con ocho cuadrados de papel. Los seis vértices del octaedro están en 3 cuadrados.
|
 |
Construcción de un cubo con cartulina. Dentro de él podemos poner un octaedro de origami. Una idea interesante asociada a esta construcción es la dualidad de cubo y octaedro.
|
 |
Presentación de los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro.
|
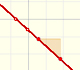 |
Dos puntos determinan una línea recta. Como función son las funciones afines. Estudiaremos la pendiente de la recta y como podemos obtener la ecuación de la recta que pasa por dos puntos. Estudiaremos el corte con el eje de abcisas.
|
24 de Marzo de 2020
Construcción de poliedros: Pequeño dodecaedro estrellado
 |
Construcción de un pequeño dodecaedro estrellado como metáfora del confinamiento que estamos viviendo por la pandemia del coronavirus COVID-19.
|
3 de Marzo de 2020
Kepler y el dodecaedro rómbico
 |
Kepler relaciona el dodecaedro rómbico con el apilamiento de balas de cañón. Si se comprime un determinado apilamiento, las balas se deforman en este poliedro.
|
28 de Febrero de 2020
Poliedros
 |
Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.
|
10 de Febrero de 2020
Cálculo mental: Polinomios
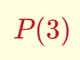 |
Aplicación para practicar el concepto de valor numérico de un polinomio de grado 1.
|
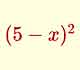 |
Aplicación para practicar las identidades notables.
|
20 de Enero de 2020
Cálculo mental: Polinomios
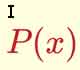 |
Aplicación para practicar sumas de polinomios de grado 1.
|
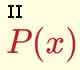 |
Aplicación para practicar multiplicaciones de polinomios de grado 1 por un número entero.
|
9 de Diciembre de 2019
Cálculo mental: Potencias
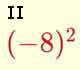 |
Aplicación para practicar cálculo mental con operaciones con potencias de números enteros. Potencia de una potencia y división de potencias.
|
4 de Noviembre de 2019
Cálculo mental: Potencias
 |
Aplicación para practicar cálculo mental con operaciones con potencias de números naturales.
|
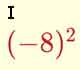 |
Aplicación para practicar cálculo mental con operaciones con potencias de números enteros.
|
30 de Septiembre de 2019
Geometría: Taller de Talento Matemático Zaragoza. XVI edición
 |
Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.
|
1 de Abril de 2019
Cálculo mental: Factorización de polinomios de grado 2
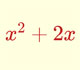 |
Aplicación para practicar cálculo mental con polinomios de grado 2. Factorizaciones.
|
18 de Marzo de 2019
Cálculo mental: Ecuaciones de grado 2
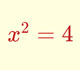 |
Aplicación para practicar cálculo mental con ecuaciones de grado 2 sencillas. En particular estudiamos ecuaciones incompletas.
|
25 de Febrero de 2019
Cálculo mental: Ecuaciones
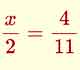 |
Aplicación para practicar cálculo mental con ecuaciones de primer grado con productos y fracciones. Intervienen tres números, como en la regla de tres.
|
18 de Febrero de 2019
Cálculo mental: Ecuaciones
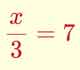 |
Aplicación para practicar cálculo mental con ecuaciones de primer grado con productos y fracciones.
|
11 de Febrero de 2019
Cálculo mental: Ecuaciones
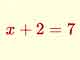 |
Aplicación para practicar cálculo mental con ecuaciones de primer grado en las que intervienen sumas y restas.
|
4 de Febrero de 2019
Cálculo mental: Porcentajes
 |
Aplicación para practicar cálculo mental sobre porcentajes sencillos.
|
28 de Enero de 2019
Cálculo mental: Fracciones
 |
Aplicación para practicar cálculo mental con operaciones fracciones: simplificación y sumas.
|
 |
Aplicación para practicar cálculo mental con operaciones fracciones: multiplicación.
|
21 de Enero de 2019
Cálculo mental: Números enteros
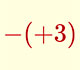 |
Aplicación para practicar cálculo mental con operaciones con números enteros.
|
7 de Enero de 2019
Historia: Kepler, el volumen de un barril de vino. Otra mirada
 |
Kepler fue uno de los matemáticos que contribuyeron al origen del cálculo integral. Uso técnicas infinitesimales para calcular áreas y volúmenes. En esta página repasamos un problema de optimización.
|
3 de Diciembre de 2018
Historia: Kepler, el volumen de un barril de vino
 |
Traducción del artículo 'Kepler: The Volume of a Wine Barrel' publicado en 2012 en Convergence ('Convergence: Where Mathematics, History, and Teaching Interact'), revista digital de la Mathematical Association of America.
|
12 de Noviembre de 2018
Geometría: El teorema de Pascal
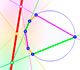 |
Si se inscribe en una circunferencia un hexágono, los puntos de intersección de lados opuestos son colineales.
|
8 de Octubre de 2018
Geometría: Icosaedro dentro de un octaedro
 |
Un icosaedro se puede poner dentro de un octaedro de modo que sus 12 vértices estén en las 12 aristas del octaedro. Dos construcciones nos ayudan a comprender esta relación y, gracias a ella, calcularemos el volumen del icosaedro.
|
25 de Septiembre de 2018
Geometría: Taller de Talento Matemático Zaragoza. XV edición
 |
Material para la sesión del TTM (Zaragoza, el 19 de Octubre de 2018). Diferentes construcciones del icosaedro nos ayudan a comprender sus propiedades. El objetivo principal es disfrutan construyendo poliedros.
|
17 de Septiembre de 2018
Geometría: semejanza
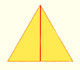 |
Los triángulos equiláteros son figuras semejantes. Si calculamos el área de un solo triángulo equilátero, por semejanza, sabremos el área de cualquier triángulo equilátero. Repasaremos relaciones entre longitudes y áreas de figuras semejantes aplicadas a este caso particular.
|
10 de Septiembre de 2018
Geometría: Sólidos platónicos
 |
Presentación de los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro.
|
 |
Estudiamos el concepto de dualidad de poliedros aplicado a los sólidos platónicos. El cubo y el octaedro son duales, el icosaedro y el dodecaedro son duales y el tetraedro decimos que es autodual.
|
14 de Mayo de 2018
Historia: Durero y las elipses
 |
Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.
|
 |
Durero nos mostró un método excelente para dibujar elipses pero cometió un pequeño error. La intuición parece decirnos que la sección de un cono tiene forma de huevo. Podemos probar, usando conceptos básicos, que la elipse tiene dos ejes de simetría.
|
7 de Mayo de 2018
Geometría: Elipses
 |
La sección de un cilindro por un plano que corta al eje del cilindro en un punto es una elipse. Probamos este resultado usando las esferas de Dandelin.
|
2 de April de 2018
Geometría e Historia
 |
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro aumentado.
|
 |
En esta segunda versión del rombicuboctaedro aumentado podemos separar las pirámides y ver el interior de la figura. Luca Pacioli escribió que 'podemos ver el interior solo con nuestra imaginación'. La aplicación interactiva solo nos ayuda a ello.
|
 |
A partir de un rombicuboctaedro podemos añadir pirámides a sus caras. Obtenemos un precioso poliedro que parece una estrella.
|
12 de Febrero de 2018
Geometría: Pseudo rombicuboctaedro
 |
También llamado girobicúpula cuadrada elongada. Es muy parecido al rombicuboctaedro pero es menos simétrico.
|
29 de Enero de 2018
Geometría: Triángulos
 |
Demostración dinámica e interactiva del teorema de Pitágoras por Hermann Baravalle.
|
8 de Enero de 2018
Geometría: Triángulos
 |
Demostración dinámica e interactiva del teorema de Pitágoras, inspirada en la de Euclides.
|
11 de Diciembre de 2017
Geometría del Espacio: Esferas y cilindros
 |
Esta proyección tiene la propiedad de preservar el área. El área de la esfera es igual al área lateral del cilindro circunscrito. Conociendo el área de la esfera podemos deducir su volumen, tal como hizo Arquímedes.
|
27 de Noviembre de 2017
Geometría del Espacio: la Tierra
 |
Un mapa básico de la Tierra como una esfera. Sistema de Coordenadas Geográfico: Latitud, longitud.
|
19 de Noviembre de 2017
Geometría del Espacio: Esfera de Campanus
 |
Estudiamos un tipo de poliedros inscritos en una esfera, en particular la llamada esfera de Campanus que fue muy popular durante el Renacimiento y que Luca Pacioli llamó Septuaginta.
|
13 de Noviembre de 2017
Historia: Leonardo da Vinci
 |
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación del poliedro de 72 caras (Septuaginta) también conocido como esfera de Campanus de Novara.
|
25 de Septiembre de 2017
Geometría: Taller de Talento Matemático de Zaragoza. XIV edición
 |
Material para la sesión del TTM (Zaragoza, el 20 de Octubre de 2017). El objetivo principal es disfrutar con las Matemáticas y fomentar la construcción de poliedros por su valor estético y también porque nos facilitan la comprensión de resultados matemáticos.
|
18 de Septiembre de 2017
Probabilidad: Distributiones normales
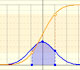 |
Calculamos probabilidades de intervalos simétricos en torno a la media en distribuciones normales.
|
11 de Septiembre de 2017
Probabilidad: Distributiones normales
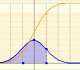 |
La función de distribución (acumulada) de una variable aleatoria X, evaluada en x, es la probabilidad de que X tome valores menores o iguales que x. En esta página estudiamos las distribuciones normales.
|
5 de Junio de 2017
Geometría: Dodecaedro rómbico
 |
Una cadena de seis pirámides puede plegarse hacia dentro y formar un cubo y puede plegarse hacia fuera y colocarse sobre otro cubo y formar un dodecaedro rómbico.
|
15 de Mayo 2017
Geometría: Construcción de poliedros
 |
Microarquitectura es un juego de construcción desarrollado por Sara San Gregorio. Podemos jugar con él y construir muchas estructuras inspiradas en poliedros.
|
3 de Mayo de 2017
Geometría: Dodecaedro rómbico
 |
Podemos llenar el espacio con dodecaedros rómbicos sin dejar huecos.
|
3 de Abril de 2017
Geometría: Dodecaedro rómbico
 |
Podemos construir un dodecaedro rómbico añadiendo seis pirámides a un cubo. Este hecho tiene interesantes consecuencias.
|
6 de Marzo de 2017
Geometría: Dodecaedro rómbico
 |
Añadiendo seis pirámides a un cubo podemos construir nuevos poliedros que tienen veinticuatro caras triángulares. Para unas determinadas pirámides obtenemos un dodecaedro rómbico que tiene doce caras rómbicas.
|
20 de Febrero 2017
Geometría: Construcción de poliedros
 |
Construcción del cubo y del octaedro con impresión 3D. El cubo y el octaedro son poliedros duales.
|
6 de Febrero de 2017
Geometría: Dodecaedro rómbico
 |
Queremos cerrar un prisma hexagonal como lo hacen las abejas, usando tres rombos iguales. ¿Qué forma deben tener estos tres rombos para cerrar el prisma con la menor superficie?
|
16 de Enero de 2017
Geometría: Construcción de poliedros
 |
Construcción del tetraedro con impresión 3d. El tetraedro es un poliedro autodual. El centro del tetraedro.
|
9 de Enero de 2017
Geometría: Dodecaedro rómbico
 |
La Humanidad ha estdo siempre fascinada por cómo las abejas construyen sus panales. Kepler relacionó la forma de los panales con un poliedro que llamamos dodecaedro rómbico.
|
5 de Diciembre de 2016
Geometría y Arte: Bruno Munari
 |
El diseñador italiano Bruno Munari pensó 'Acona Biconbi' como un trabajo de escultura. También es un juego de construcción con el que podemos jugar con colores y formas.
|
21 de Noviembre de 2016
Geometría: Construcción de poliedros
 |
Técnica simple para construir poliedros pegando discos de cartulina.
|
7 de Noviembre de 2016
Geometría: Curvas
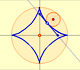 |
La astroide es un caso particular de una familia de curvas que llamamos hipocicloides.
|
19 de Septiembre de 2016
Geometría: Taller de Talento Matemático de Zaragoza. XIII edición
 |
Material para la sesión del TTM (Zaragoza, el 10 de marzo de 2023). Con plantillas para descargar y construir varias figuras geométricas.
|
5 de Septiembre de 2016
Geometría: Curvas
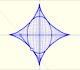 |
La astroide es la envolvente de un segmento de longitud constante cuyos extremos se mueven sobre dos rectas perpendiculares. También es la envolvente de una familia de elipses con la propiedad de que la suma de sus ejes es constante.
|
1 de Agosto de 2016
Geometría: Elipses
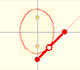 |
Si un segmento de longitud fija se mueve de modo que sus extremos están en dos rectas perpendiculares, cualquier punto del segmento traza una elipse.
|
4 de Julio de 2016
Geometría: Elipses
 |
El elipsógrafo es un aparato mecánico que se usa para dibujar elipses.
|
6 de Junio de 2016
Geometría: Piritoedro
 |
Si plegamos los seis tejadillos del dodecaedro dentro de un cubo queda un espacio vacío en el interior. Este espacio es un dodecaedro no regular con todas sus caras pentagonales iguales. Este dodecaedro es un caso particular de piritoedro.
|
2 de Mayo de 2016
Geometría: El dodecaedro y el cubo
 |
Se puede inscribir un cubo en un dodecaedro y podemos ver el dodecaedro como un cubo con seis 'tejados' añadidos uno en cada cara. Estos seis tejados del dodecaedro se pueden plegar en un cubo.
|
4 de Abril de 2016
Historia: Leonardo da Vinci
 |
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro.
|
7 de Marzo de 2016
Geometría: Desarrollo plano del tetraedro
 |
El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
|
1 de Febrero de 2016
Geometría: Desarrollo plano del octaedro
 |
El primer dibujo del desarrollo plano del octaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
|
18 de Enero de 2016
Historia: Leonardo da Vinci
 |
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro.
|
31 de Diciembre de 2015
Actualizaciones complejos: Multiplicación de números complejos
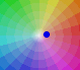 |
Geométricamente, la multiplicación por un complejo es una transformación del plano que consiste en una rotación y una expansión o contracción (rotación dilatativa).
|
7 de Diciembre de 2015
Actualizaciones complejos: Multiplicación de números complejos
 |
Se puede ver como una rotación dilatativa.
|
16 de Noviembre de 2015
Actualizaciones análisis: Sucesiones geométricas
 |
Representación gráfica de progresiones geométricas. Suma de los términos de una sucesión geométrica. Series geométricas.
|
2 de Noviembre de 2015
Historia: Durero y las transformaciones
 |
Durero estudió transformaciones aplicadas a figuras para, por ejemplo, modificar caras y generar otras caras o caricaturas. Algunas de estas transformaciones son afinidades.
|
29 de Septiembre de 2015
Geometría: Taller de Talento Matemático de Zaragoza. XII edición
 |
Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.
|
21 de Septiembre de 2015
Geometría: Triángulos
 |
Demostración muy bonita y visual de Conway. Podemos jugar con una animación interactiva y ver los diferentes pasos de la demostración.
|
14 de Septiembre de 2015
Actualizaciones geometría: Triángulos
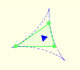 |
El triángulo equilátero determinado por la deltoide de Steiner tiene los lados paralelos al triángulo de Morley pero con orientación opuesta.
|
7 de Septiembre de 2015
Actualizaciones geometría: Triángulos
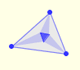 |
Los tres puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera son los vértices de un triángulo equilátero (Triángulo de Morley).
|
29 de Junio de 2015
Actualizaciones geometría: Triángulos
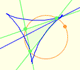 |
La envolvente de las rectas de Simson-Wallace de un triángulo es una curva con tres cúspides que se llama Deltoide de Steiner.
|
8 de Junio de 2015
Actualizaciones geometría: Triángulos
 |
Demostración interactiva de que los tres puntos que determinan cada recta de Wallace-Simson están alineados.
|
6 de Abril de 2015
Geometría: Espirales
 |
Hay infinitas espirales equiangulares que pasan por dos puntos.
|
2 de Marzo de 2015
Análisis: Funciones definidas a trozos
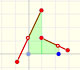 |
En general, las funciones lineales a trozos no son continuas. Hay puntos en los que un pequeño cambio en la x produce un salto en el valor de la función.
|
2 de Febrero de 2015
Análisis: Funciones definidas a trozos
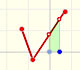 |
Una función continua lineal a trozos se define con varios segmentos o rayos que están unidos de un modo continuo, sin saltos entre ellos.
|
12 de Enero de 2015
Análisis: Funciones definidas a trozos
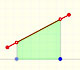 |
Como una introducción a las funciones lineales a trozos estudiamos el caso más sencillo, las funciones lineales restringidas a un intervalo abierto: sus gráficas son segmentos.
|
1 de Diciembre de 2014
Análisis: Funciones definidas a trozos
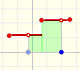 |
Una función constante a trozos (o función escalonada) está definida por varias subfunciones que son funciones constantes.
|
27 de Octubre de 2014
Geometría
 |
Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.
|
20 de Octubre de 2014
Geometría: Construcción de poliedros
 |
Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.
|
6 de Octubre de 2014
Geometría
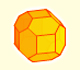 |
Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.
|
7 de Julio de 2014
Geometría
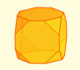 |
Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.
|
2 de Junio de 2014
Geometría
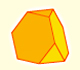 |
El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.
|
28 de Abril de 2014
Geometría: Construcción de Poliedros, cuboctaedro y dodecaedro rómbico
 |
Material para la sesión del TTM (Zaragoza, 8 de marzo de 2024). Con plantillas para descargar y construir dodecaedros rómbicos y celdas de abejas.
|
7 de Abril de 2014
Historia: Leonardo da Vinci
 |
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su tetraedro truncado.
|
3 de Marzo de 2014
Análisis: Funciones Racionales
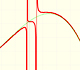 |
Podemos añadir un polinomio a una función racional propia. El comportamiento asintótico de esta función racional será muy parecido al del polinomio.
|
3 de Febrero de 2014
Análisis: Funciones Racionales
 |
Para valores grandes en valor absoluto de la variable x algunas funciones se comportan como una recta oblicua. A esta recta la llamamos asíntota oblicua de la función.
|
7 de Enero de 2014
Análisis: Funciones Racionales
 |
Si el denominador de una función racional es un polinomio de grado 2 la función tiene dos, una o ninguna singularidad real (asíntotas verticales y singularidades evitables).
|
2 de Diciembre 2013
Análisis: Funciones Racionales
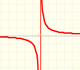 |
Las funciones racionales son las que pueden escribirse como cociente de dos polinomios. Las funciones racionales lineales son las más sencillas de este tipo.
|
20 de Octubre 2013
Analisis: Convergencia de Series, el criterio de la integral
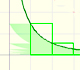 |
A partir de una función positiva decreciente podemos definir series y aplicar el test de la integral. El test de la integral es un criterio que nos puede ayudar a decidir si una serie converge o diverge. Además, si la serie converge nos dará cotas.
|
7 de Octubre 2013
Historia: construcción de Durero de un pentágono
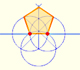 |
En su libro 'Underweysung der Messung' Durero dibujó un pentágono no regular con regla y compás con apertura fija. Es una construcción simple y una muy buena aproximación de un pentágono regular.
|
16 de Septiembre 2013
Geometría: Desarrollos planos de cuerpos geométricos
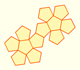 |
El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
|
2 de Septiembre 2013
Geometría: Volumen de un dodecaedro regular
 |
Descomponiendo adecuadamente un dodecaedro podemos obtener fácilmente su volumen.
|
1 de Julio 2013
Geometría: Dibujo de un pentágono regular
 |
Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.
|
3 de Junio 2013
Geometría: Ángulos de 15 grados
 |
Usando regla y compás podemos dibujar ángulos de 15 grados. Son ejemplos básicos de las propiedades de los ángulos central e inscrito en una circunferencia.
|
6 de Mayo 2013
Geometría: Proporción áurea
 |
La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.
|
1 de Abril 2013
Análisis: Teorema Fundamental del Cálculo
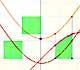 |
El Segundo Teorema Fundamental del Cálculo nos proporciona una herramienta muy potente para calcular integrales definidas (si conocemos una primitiva o antiderivada de la función).
|
4 de Marzo 2013
Análisis: Teorema Fundamental del Cálculo
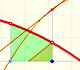 |
El Teorema Fundamental del Cálculo afirma que toda función continua tiene una antiderivada y nos muestra cómo construir una usando la integral.
|
18 de Febrero 2013
Análisis: Potencias y polinomios
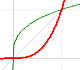 |
Potencias con exponente natural son funciones importantes pues son la base de los polinomios. Sus funciones inversas son las raíces que son funciones potencia con exponente racional positivo.
|
4 de Febrero 2013
Análisis: Integral
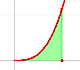 |
La integral de las funciones potencia era conocida por Cavalieri para n=1 hasta n=9. Fermat, entre otros, fue capaz de resolver este problema. Su técnica es un buen ejemplo del uso de progresiones geométricas.
|
3 de Enero 2013
Análisis: Integral
 |
Las funciones monótonas definidas en intervalos cerrados son interables. En estos casos podemos acotar el error que cometemos al aproximar la integral usando rectángulos.
|
3 de Diciembre 2012
Análisis: Integral
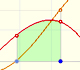 |
Si consideramos el límite inferior de integración fijado y podemos calcular la integral definida para diferentes valores del límite superior de integración entonces podemos definir una nueva función: una integral indefinida de f.
|
12 de Noviembre 2012
Análisis: Integral
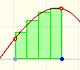 |
La integral formaliza el concepto intuitivo de área. Para su definición aproximamos el área usando rectángulos.
|
22 de Octubre 2012
Análisis: Funciones polinómicas y derivada
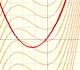 |
Si la derivada de F(x) es f(x) decimos que F es una antiderivada de f. También decimos que F es una primitiva o una integral indefinida de f.
|
1 de Octubre 2012
Análisis: Potencias y polinomios
 |
Se trata de encontrar el polinomio de menor grado que pasa por una serie de puntos del plano. Es un problema de interpolación que aquí resolvemos usando los polinomios de Lagrange.
|
17 de Septiembre 2012
Análisis: Funciones polinómicas e integral
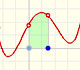 |
Estudiamos algunos conceptos básicos sobre integración aplicados a funciones polinómicas de cualquier grado. Las funciones integrales de funciones polinómicas son polinomios de un grado más que la función original.
|
27 de Agosto 2012
Análisis: Funciones polinómicas e integral
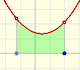 |
Calcular el área bajo una parábola es mucho más difícil que calcular áreas bajo una recta. Aquí mostramos como aproximar el área usando rectángulos y que una función integral de un polinomio de grado 2 es un polinomio de grado 3.
|
6 de Agosto 2012
Análisis: Funciones polinómicas e integral
 |
Es fácil calcular el área bajo una línea recta y el eje de abcisas. Es un primer ejemplo de integración que nos permite entender la idea e introducir algunos conceptos básicos: integral como área, límites de integración, áreas positivas y negativas.
|
18 de Junio 2012
Análisis: Funciones polinómicas y derivada
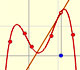 |
Los polinomios de Lagrange son polinomios que pasan por n puntos dados. Usamos los polinomios de Lagrange para explorar funciones polinómicas más generales y sus derivadas.
|
28 de Mayo de 2012
Análisis: Funciones polinómicas y derivada
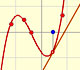 |
La derivada de una función cúbica es una función cuadráticas, es decir, una parábola
|
7 de Mayo de 2012
Análisis: Funciones polinómicas y derivada
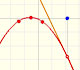 |
La derivada de una función cuadrática es una función afín, es decir, es una línea recta.
|
16 de Abril de 2012
Análisis: Funciones polinómicas y derivada
 |
La derivada de una función lineal es la función constante cuyo valor es la pendiente de la recta.
|
25 de Marzo de 2012
Geometría: Construcción de poliedros. Técnicas sencillas
 |
Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.
|
20 de Marzo de 2012
Geometría: Construcción de poliedros. Técnicas sencillas
 |
Breve introducción a una serie de páginas sobre técnicas sencillas de construcción de poliedros. Un poco de historia.
|
 |
Dibujar, recortar y pegar desarrollos de poliedros sobre cartulina. Podemos empezar por un cubo y un tetraedro.
|
 |
Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.
|
 |
El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.
|
 |
A partir de tres rectángulos áureos entrelazados podemos construir un icosaedro.
|
 |
Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.
|
 |
Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.
|
 |
Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.
|
20 de Febrero de 2012
Geometría: desarrollos planos de cuerpos geométricos
 |
Desarrollos planos de conos truncados por un plano oblicuo. La sección es una elipse.
|
30 de Enero de 2012
Geometría: desarrollos planos de cuerpos geométricos
 |
Desarrollos planos de conos y troncos de cono. Cálculo del área lateral de estas figuras.
|
9 de Enero de 2012
Geometría: desarrollos planos de cuerpos geométricos
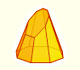 |
Desarrollos planos de pirámides truncadas por un plano oblicuo.
|
2 de Diciembre de 2011
Geometría: desarrollos planos de cuerpos geométricos
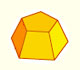 |
Desarrollos planos de pirámides y de troncos de pirámide de base regular con diferentes números de lados.
|
18 de Noviembre de 2011
Personal: El Juego de la Vida con fotos de Naturaleza
 |
En esta nueva versión del Juego de la Vida de John H. Conway, podemos ver más de 100 fotografía de Naturaleza. Cada vez que se ejecuta la aplicación se muestran 36 fotos elegidas al azar.
|
4 de Noviembre de 2011
Geometría: desarrollos planos de cuerpos geométricos
 |
La sección de un cilindro por un plano es una elipse. Estas figuras se llaman segmentos cilíndricos o cilindros truncados y pueden desarrollarse en el plano.
|
21 de Octubre de 2011
Geometría: desarrollos planos de cuerpos geométricos
 |
Los cilindros son superficies de revolución que pueden desarrollarse en un plano. Se explica cómo calcular la superficie lateral y total de un cilindro.
|
7 de Octubre de 2011
Geometría: desarrollos planos de cuerpos geométricos
 |
Prismas con base regular o irregular cortados por un plano no paralelo a la base y sus desarrollos planos.
|
30 de Septiembre de 2011
Geometría: desarrollos planos de cuerpos geométricos
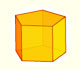 |
Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.
|
15 de Septiembre de 2011
Análisis
 |
Nueva versión de varias páginas sobre los Polinomios de Taylor. Mejorados los mathlets y más imágenes. Empezamos estudiando varias funciones reales pero necesitamos ir al plano complejo para comprender mejor el concepto.
|
30 de Agosto de 2011
Probabilidad
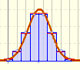 |
En algunos casos, una distribución Binomial puede aproximarse con una distribución Normal con la misma media y varianza.
|
3 de Agosto de 2011
Probabilidad
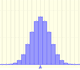 |
La distribución binomial modela una situación en la que hay n ensayos independientes con una probabilidad constante de éxito.
|
26 de Junio de 2011
Geometría
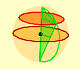 |
Calculamos el área de las secciones de una esfera usando el Teorema de Pitágoras. También estudiamos la relación con la media geométrica o el teorema de la altura de triángulos rectángulos. Usaremos este resultado en aplicaciones del Teorema de Cavalieri.
|
29 de Mayo de 2011
Historia: Arquímedes y el área de la elipse
 |
En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.
|
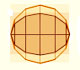 |
En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.
|
29 de Mayo de 2011
Geometria: Elipses
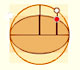 |
Transformando una circunferencia podemos obtener una elipse (como hizo Arquímedes para calcular su área). A partir de la ecuación de la circunferencia deducimos la de la elipse.
|
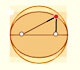 |
Una elipse tiene dos focos y la suma de las distancias de cualquier punto de la elipse a los dos focos es una constante.
|
29 de Abril de 2011
Dibujos de Leonardo da Vinci para 'La Divina Proporción' de Luca Pacioli
 |
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.
|
 |
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.
|
 |
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.
|
 |
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro estrellado (que Kepler llamó stella octangula).
|
29 de Abril de 2011
Volúmenes de poliedros
 |
El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.
|
 |
El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices
|
 |
El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.
|
 |
El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.
|
24 de Febrero de 2011
Geometría
 |
El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.
|
21 de Enero de 2011
Geometría
 |
A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.
|
6 de Enero de 2011
Circunferencia
 |
Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.
|
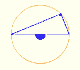 |
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso I: Cuando el arco es una semicircunferencia el ángulo inscrito es recto.
|
 |
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso II: Cuando una cuerda de las que forman el ángulo inscrito es un diámetro.
|
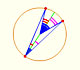 |
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Prueba del caso general.
|
18 de Septiembre de 2010
Complejos
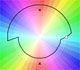 |
Una multifunción puede tener más de un punto de ramificación. La multifunción considerada en esta página tiene dos valores y dos puntos de ramificación.
|
26 de Julio de 2010
Geometria
 |
El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.
|
15 de Julio de 2010
Complejos
 |
El concepto de función puede extenderse permitiendo que f(z) tenga diferentes valores para un valor z. En este caso decimos que f es una función multivaluada o multifunción.
|
11 de Junio de 2010
Geometría
 |
Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.
|
7 de Junio de 2010
Geometría
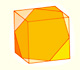 |
Podemos cortar un cubo por la mitad con un plano de modo que la sección sea un hexágono regular. Ocho de estos medios cubos forman un octaedro truncado.
|
 |
Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.
|
2 de Junio de 2010
Análisis
 |
La serie geométrica de razón 1/2 es convergente. Esta serie se puede representar usando un rectángulo y dividiéndolo por la mitad sucesivamente. Aquí usamos una proporción de modo que todos los rectángulos son semejantes.
|
25 de Mayo de 2010
Análisis
 |
Algunas series geométricas se pueden sumar fácilmente. Podemos ver un ejemplo muy intuitivo cuando la razón es 1/4.
|
6 de Mayo de 2010
Geometría
 |
El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.
|
28 de Abril de 2010
Geometría
 |
El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
|
21 de Abril de 2010
Geometría
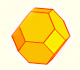 |
El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.
|
29 de Marzo de 2010
Complejos
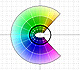 |
La función coseno compleja extiende la función real al plano complejo. Es una función periódica que comparte varias propiedades con la función real.
|
 |
La función coseno compleja transforma rectas horizontales en elipses cofocales.
|
26 de Marzo de 2010
Historia
 |
Kepler usó una aproximación infinitesimal intuitiva para calcular el área de un círculo.
|
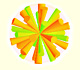 |
Kepler estudió el volumen y la superficie de una esfera. La esfera puede considerarse formada por conos cuya altura es el radio de la esfera. Entonces el volumen de la esfera será la suma de todos esos conos. Así obtiene la relación entre la superficie de la esfera y su volumen.
|
 |
Kepler fue uno de los matemáticos que contribuyeron al origen del cálculo integral. Uso técnicas infinitesimales para calcular áreas y volúmenes.
|
 |
Cavalieri enunció el teorema que conocemos como Principio de Cavalieri. Usando el Principio de Cavalieri podemos calcular el volumen de una esfera
|
8 de Diciembre de 2009
Historia
 |
Estudiando el volumen de un barril, Kepler se planteó un problema de máximo en 1615.
|
21 de Noviembre de 2009
Historia
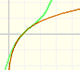 |
Mercator publicó su famosa serie para la función logaritmo en 1668. Euler descubrió una serie práctica para el cálculo.
|
16 de Noviembre de 2009
Historia
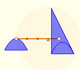 |
Arquímedes explica en 'El Método' cómo se puede utilizar la ley de la palanca para descubrir cuál es el área de un segmento parabólico.
|
26 de Octubre de 2009
Historia
 |
Podemos ver el teorema de Pitágoras en un mosaico. Es una demostración gráfica sencilla del teorema de Pitágoras que vemos en suelos cuando se combinan cuadrados de dos tamaños.
|
14 de Octubre de 2009
Complejos
 |
La inversión preserva la magnitud de los ángulos pero invierte el sentido. Circunferencias ortogonales se transforman en circunferencias ortogonales
|
6 de Octubre de 2009
Complejos
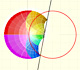 |
La inversión es una transformación del plano que transforma rectas y circunferencias en rectas y circunferencias.
|
21 de Septiembre de 2009
Complejos
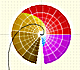 |
La función exponencial compleja extiende la función exponencial real al plano complejo.
|
14 de Septiembre de 2009
Personal
 |
En esta nueva versión del Juego de la Vida de John H. Conway, se eligen las fotografías al azar de entre más de 100 fotografías de Naturaleza.
|
1 de Septiembre de 2009
Polinomios de Taylor
 |
La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.
|
 |
La función coseno compleja tiene un desarrollo de Taylor que converge en todo el plano complejo.
|
12 de Junio de 2009
Polinomios de Taylor
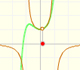 |
La función tiene dos singularidades reales, en -1 y en 1. Los polinomios de Taylor aproximan la función entre en un intervalo simétrico respecto al centro del desarrollo. Su radio es la distancia a la singulardidad más próxima.
|
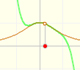 |
La función es continua y no tiene singularidades reales. Sin embargo, los polinomios de Taylor sólo aproximan la función en un intervalo. Entenderemos un poco mejor este comportamiento estudiando una función compleja.
|
 |
Podemos estudiar la aproximación a esta función por el polinomio de Taylor y su convergencia en el círculo de convergencia.
|
22 de Mayo de 2009
Polinomios de Taylor
 |
Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.
|
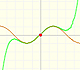 |
Al aumentar el grado del polinomio de Taylor se aproxima a la función seno en un intervalo más y más amplio.
|
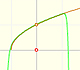 |
La función no está definida para valores menores que -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
|
 |
La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
|
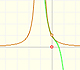 |
La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
|
9 de Mayo de 2009
Personal, nueva seccion
 |
El Juego de la Vida, inventado por John H. Conway, es uno de los autómatas celulares bidimensionales más famosos. Usando la colonia de un deslizador presentamos una serie de fotografías de Naturaleza..
|
15 de Marzo de 2009
Geometría del espacio
 |
Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.
|
24 de Enero de 2009
Transformaciones
 |
Durero estudió transformaciones aplicadas a figuras para, por ejemplo, modificar caras y generar otras caras o caricaturas. Algunas de estas transformaciones son afinidades.
|
 |
Cuadro en el que, entre otras muchas cosas, podemos ver una anamorfosis de una calavera
|
16 de Enero de 2009
Geometría del espacio
 |
El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
|
5 de Enero de 2009
Sucesiones y series
 |
La constante de Euler se define como una serie convergente.
|
17 de Noviembre de 2008
Geometría del espacio
 |
Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.
|
 |
Descomponiendo adecuadamente un dodecaedro podemos obtener fácilmente su volumen.
|
23 de Octubre de 2008
Geometría del espacio
 |
El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.
|
 |
Haciendo adecuadamente secciones en un tetraedro obtenemos rectángulos y, en algún caso, un cuadrado. Podemos calcular el área de esas secciones.
|
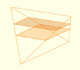 |
En su artículo 'Two Surprising Theorems on Cavallieri Congruence' (Dos teoremas sorprendentes sobre la congruencia de Cavalieri), Howard Eves describe un tetraedro muy interesante. En esta página calculamos las áreas de sus secciones y su volumen.
|
 |
Calculamos el área de las secciones de una esfera usando el Teorema de Pitágoras. También estudiamos la relación con la media geométrica o el teorema de la altura de triángulos rectángulos.
|
 |
El tetraedro de Howard Eves es congruente Cavalieri con una esfera dada. Podemos ver que las secciones correspondientes tienen áreas iguales. Por lo tanto, el volumen de la esfera es el mismo que el volumen del tetraedro. Sabemos calcular el volumen del tetraedro luego ya sabemos el volumen de la esfera (usando una congruencia sorprendente).
|
28 de Octubre de 2007
Complejos
 |
Un polinomio de grado 2 tiene dos raíces o ceros. En esta representación podemos ver los óvalos de Cassini y la lemniscata.
|
 |
Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.
|
 |
Tenemos más control sobre qué partes del plano complejo se representa con colores.
|
 |
Una primera aproximación a estas transformaciones. Representación de dos haces coaxiales de circunferencias ortogonales.
|
15 de Octubre de 2007
Variables aleatorias
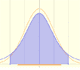 |
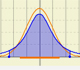
La distribución t de Student fue estudiada por Gosset y se aproxima a una distribución normal.
|
 |
|
8 de Septiembre de 2007
Variables aleatorias
 |
La distribución binomial modela una situación en la que hay n ensayos independientes con una probabilidad constante de éxito.
|
 |
La distribución de Poisson también se llama distribución de sucesos raros.
|
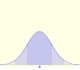 |
Las distribucines normales fueron estudiadas por Gauss. Son variables aleatorias continuas (la variable puede tomar cualquier valor real). La función de densidad tiene forma de campana.
|
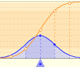 |
Una propiedad importante de las distribuciones normales es que si consideramos intervalos centrados en la media y con una longitud proporcional a la desviación típica, la probabilidad de estos intervalos es constante independientemente de la distribución normal considerada.
|
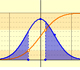 |
Cálculo aproximado de probabilidades de diferentes intervalos en distribuciones normales.
|
26 de Agosto de 2007
Exponenciales y logaritmos
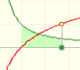 |
Integrando la hipérbola equilátera podemos definir una nueva función que es el logaritmo natural.
|
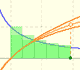 |
El número e se puede definir como áquel cuyo logaritmo es 1. Partiendo de esta definición podemos aproximar su valor.
|
 |
El número e, la base de los logaritmos naturales, se puede definir como una integral o como el límite de una sucesión relacionada con el interés compuesto. Ambas definiciones coinciden.
|
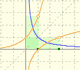 |
Partiendo de la definición de logaritmo podemos definir la exponencial como su inversa.
|
 |
Diferentes hipérbolas permiten definir logaritmos y exponenciales (sus inversas).
|
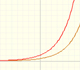 |
Estudiamos varias propiedades de las funciones exponenciales, sus derivadas y una introducción al número e.
|
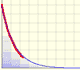 |
Las funciones exponenciales pueden modelar la desintegración radioactiva.
|
8 de Marzo de 2007
Se inició la publicación de MatematicasVisuales.
|