Ya hemos comentado que Kepler concibe el dodecaedro rómbico desde diferentes puntos de vista. Cada uno de ellos
nos aporta una visión complementaria del poliedro.
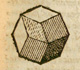
Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.
Kepler establece una sorprendente relación entre este poliedro y el problema de apilamiento óptimo de balas de cañon.
El origen de la cuestión de cómo apilar balas de cañón en las cubiertas de los barcos proviene de una carta que le envía a Kepler el
astrónomo y matemático inglés Thomas Harriot. Harriot era amigo de Sir Walter Raleigh y, por lo tanto, la cuestión pretende responder
un problema práctico.
Este asunto le lleva a Kepler a investigar empaquetamientos óptimos de esferas y a enunciar lo que concemos como "Conjetura de Kepler".
Esto nos llevaría por otros derroteros pero lo que queremos destacar aquí es la relación que establece entre el apilamiento de balas y el dodecaedro rómbico.
Para Kepler, el empaquetamiento óptimo consiste en rodear cada bala por otras seis en un capa. En las siguientes capas se trata de colocar balas en los huecos
que resultan. Esta es una explicación muy básica.
Pero entonces entra en acción la imaginación y creatividad de Kepler quién afirma que si comprimiéramos de un modo homogéneo esa estructura de balas y las
balas se deformaran se formarían dodecaedros rómbicos.
Esto hay que verlo, pensé yo. Y me propuse intentar reproducir este experimento. Resultó ser espectacular y sencillo.
Para empezar preparo 13 bolas de arcilla iguales.
En la primera capa pondremos una bola en el centro y seis alrededor. En los huecos pondremos tres bolas más encima y tres debajo.
Resulta esta estructura.
Estamos viendo que esto que estamos haciendo tiene mucho que ver con el dodecaedro rómbico que Kepler concibe a partir de los panales de la abejas.
Kepler se fija en la base de las celdas de las abejas. Allí hay tres rombos que se corresponden con las tres bolas de debajo.
Después hay seis rombos que los vemos apoyados sobre las seis caras de la celda hexagonal. Se corresponden con las seis bolas de la capa central que rodean a
una bola.
El poliedro se cierra con otros tres rombos como los de la base de la celda. Son las últimas tres bolas.
Tenemos, por lo tanto, doce bolas ordenadas de este modo y que rodean a una bola central.
Queremos presionar el conjunto. Para evitar que se peguen pongo aceite con ayuda de un pincel.
Así queda la bola central. Se ha formado un dodecaedro rómbico bastante perfecto.
Un experimento sencillo y efectivo para mostrar, una vez más, que Kepler tenía razón.
REFERENCIAS
Johannes Kepler - 'De Nive Sexangula' (Tenemos una versión bilingüe en latin e inglés en
'The Six Cornered Snowflake: a New Year's gif' - Paul Dry Books, Philadelphia, Pennsylvania, 2010.
Con notas y comentarios muy interesantes de Owen Gingerich y Guillermo Bleichmar. Las ilustraciones las realizó la matemática española Capi Corrales Rodrigáñez.
Johannes Kepler - 'Regalo de año nuevo, sobre el copo de nieve hexagonal;Strena seu de nive sexangula'.
Introducción, traducción al castellano, ilustraciones y notas, Ana García Azcárate y Ángel Requena Fraile. Editorial Avinareta.
MÁS ENLACES
El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.
El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.
Queremos cerrar un prisma hexagonal como lo hacen las abejas, usando tres rombos iguales. ¿Qué forma deben tener estos tres rombos para cerrar el prisma con la menor superficie?
Añadiendo seis pirámides a un cubo podemos construir nuevos poliedros que tienen veinticuatro caras triángulares. Para unas determinadas pirámides obtenemos un dodecaedro rómbico que tiene doce caras rómbicas.
Podemos construir un dodecaedro rómbico añadiendo seis pirámides a un cubo. Este hecho tiene interesantes consecuencias.
Una cadena de seis pirámides puede plegarse hacia dentro y formar un cubo y puede plegarse hacia fuera y colocarse sobre otro cubo y formar un dodecaedro rómbico.
Podemos llenar el espacio con dodecaedros rómbicos sin dejar huecos.
Kepler relaciona el dodecaedro rómbico con el apilamiento de balas de cañón. Si se comprime un determinado apilamiento, las balas se deforman en este poliedro.
El ángulo obtuso de las caras rómbicas del dodecaedro rómbico se conoce como ángulo de Maraldi. Solo se necesita un poco de trigonometría básica parar calcularlo.
Estudiando el empaquetamiento de esferas obtenemos el dodecaedro rómbico y el dodecaedro trapezo-rómbico. Su dual es el cuboctaedro girado.
A partir de un conocimiento básico del dodecaedro rómbico se puede calcular rápidamente la densidad del empaquetamiento óptimo de esferas.
Tetraxis es un puzle muy interesante, sencillo y bonito, diseñado por Jane y John Kostick. Estudiaremos algunas propiedades de este juego y su relación con el dodecaedro rómbico. Plantillas para construir un Tetraxis con cartulina e imanes. El rompecabezas hecho con impresión 3D.
Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.
Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.
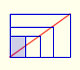
El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.
El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.
El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices
El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
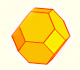
El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.
El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.
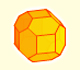
Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.
Se puede inscribir un cubo en un dodecaedro y podemos ver el dodecaedro como un cubo con seis 'tejados' añadidos uno en cada cara. Estos seis tejados del dodecaedro se pueden plegar en un cubo.
Si plegamos los seis tejadillos del dodecaedro dentro de un cubo queda un espacio vacío en el interior. Este espacio es un dodecaedro no regular con todas sus caras pentagonales iguales. Este dodecaedro es un caso particular de piritoedro.
SIGUIENTE
ANTERIOR
