En casa: actividades matemáticas sencillas
En esta página se presentan actividades matemáticas sencillas pensadas para alumnos que tengan de 9 a 13 años, aproximadamente.
En esta sección encontrarás actividades del nivel más sencillo:
Es un trabajo muy sencillo que todos podemos intentar.
Miscelánea
Iniciamos esta sección con un sencillo truco de magia.
 Magia para adivinar el pensamiento. Magia para adivinar el pensamiento.

Propuesta de dibujar unas tarjetas para hacer un truco de magia apto para los más jóvenes. Con ellas adivinaremos el pensamiento. El fundamento matemático es muy interesasnte.
 Plegado y decoración de una piraña de origami. Plegado y decoración de una piraña de origami.

Plegado y decoración de una piraña de origami. Figura muy sencilla para introducir a los más pequeños en el origami. A un paso de hacer la pajarita.
 Las torres de Hanoi. Versión sobre un cuadro de Magritte. Las torres de Hanoi. Versión sobre un cuadro de Magritte.

Las torres de Hanoi es un rompecabezas que aquí se presenta haciendo una versión sobre un cuadro de Magritte.
 Rompecabezas del enanito que desaparece. Rompecabezas del enanito que desaparece.

Conocido rompecabezas en el que al cambiar dos piezas de un dibujo desaparece uno de los enanitos. ¿Qué explicación tiene?.
Ángulos
En esta sección vamos a plantear algunas cuestiones referidas a ángulos.
 Un triángulo que es medido cuadrado. Un triángulo que es medido cuadrado.

Si doblamos un cuadrado de papel por la mitad obtenemos un triángulo. ¿Qué ángulos se han formado? ¿Cómo es el triángulo?.
Semejanza
En esta sección estudiaremos la semejanza de figuras planas y espaciales.
Es un concepto que usamos en nuestra vida cotidiana y que está relacionada con la escalas (de los planos, mapas, maquetas).
De un modo intuitivo, podemos decir que dos figuras son semejantes si 'tienen la misma forma'.
Luego iremos concretando esta expresión pero resulta que dos figuras semejantes tienen 'sus águlos ccrrespondientes iguales'.
Pero además interviene la proporcionalidad y decimos que 'sus lados correspondientes son proporcionales'.
Desarrollaremos más adelante estas ideas con detalle, pero ahora empezamos con un caso concreto, estudiando los cuadrados.
 Todos los cuadrados son semejantes Todos los cuadrados son semejantes

Todos los cuadrados son semejantes. Estudiamos la relación entre lado y diagonal de un modo intuitivo.
 Todas las circunferencias son semejantes. El número Pi. Todas las circunferencias son semejantes. El número Pi.

Todas las circunferencias son semejantes. Esta idea tan simple nos lleva a un concepto muy importante, la definición del número Pi.
El cuadrado
En esta sección estudiaremos el cuadrado y alguna de sus propiedades, por ejemplo la relación entre el lado la diagonal.
 Plegado de un cuadrado a partir de un dinA4. Plegado de un cuadrado a partir de un dinA4.

Podemos construir un cuadrado doblando y cortando un folio. Se trata de un ejercicio muy básico de origami. Mediremos la diagonal.
 Construcción de un cuadrado con pajitas con su diagonal. Construcción de un cuadrado con pajitas con su diagonal.

Podemos construir un cuadrado con pajitas de refresco. Notamos que no es rígido. Si lo deformamos obtenemos rombos. Para conseguir que sea rígido podemos añadir una pajita en la diagonal.
Circunferencia y círculo
Circunferencia y círculo son dos palabras para referirse a la misma figura. Cuando nos queremos referir a su perímetro hablamos de
circunferencia mientras que círculo lo usamos cuando nos referimos su área.
 Todas las circunferencias son semejantes. El número Pi. Todas las circunferencias son semejantes. El número Pi.

Todas las circunferencias son semejantes. Esta idea tan simple nos lleva a un concepto muy importante, la definición del número Pi.
 El área de un círculo. El área de un círculo.

Una aproximación intuitiva al área de un círculo. Para calcular el área de un círculo también necesitamos el número Pi.
 Circunferencias por dos puntos. Circunferencias por dos puntos.
Animación inspirada en el trabajo de Jean Louis Nicolet y Caleb Gattegno sobre circunferencias que pasan por dos puntos.

Animación inspirada en el trabajo de Jean Louis Nicolet y Caleb Gattegno sobre circunferencias que pasan por dos puntos.
 Circunferencias por tres puntos. Circunferencias por tres puntos.
Animación inspirada en el trabajo de Jean Louis Nicolet y Caleb Gattegno sobre circunferencias que pasan por tres puntos.

Animación inspirada en el trabajo de Jean Louis Nicolet y Caleb Gattegno sobre circunferencias que pasan por tres puntos.
Rectángulos
En esta sección vamos a estudiar dos familias de rectángulos especialmente interesantes: los rectángulos raíz cuadrada de 2 y
los rectángulos áureos.
 No todos los rectángulos son semejantes. No todos los rectángulos son semejantes.

No todos los rectángulos son semejantes pues tienen distintas formas, unos son más alargados que otros.
 Proporción del papel estándar Din A. Proporción del papel estándar Din A.
El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.
El pentágono
El pentágono es un polígono muy bonito. Está directamente relacionado con la razón áurea. Es un reto aprender a dibujarlo con
regla y compás. Las caras del dodecaedro regular son pentágonos. El pentágono también está relacionado con el icosaedro.
 Construcción de una estrellita con una tira de papel Construcción de una estrellita con una tira de papel
Partiendo de una tira de papel (que podemos cortar de cualquier revista) realizaremos esta actividad muy fácil de origami tradicional.
Nos permite introducir el pentágono y ver sus diagonales.

Actividad de origami tradicional, muy sencilla de hacer y muy bonita. Nos introduce en el conocimiento del pentágono y sus diagonales.
Curvas
Mostraremos curvas generadas haciendo rodar una circunferencia sobre una recta u otra circunferencia.
Esas curvas se llaman cicloide, hipocicloides y epicicloides.

Se presentan estas curvas con una animación de una transformación continua de la cicloide en una hipocicloide de 3 puntas llamada deltoide.
Se presenta la cicloide y se muestra una deformación continua de la cicloide en otras hipocicloides como la deltoide.
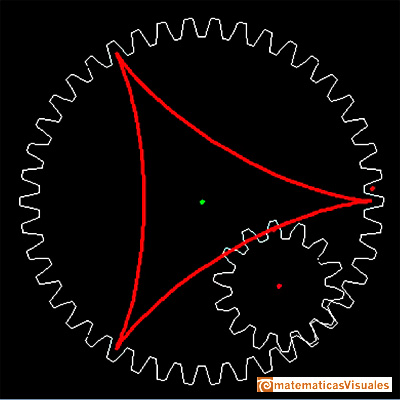
Generación mediante engranajes de varias curvas de la familia de las hipocicloides: astroide, deltoide y otras.

Más ejemplos de curvas de la familia de las hipocicloides generadas mediante engranajes.

Generación mediante engranajes de varias curvas de la familia de las epicicloides: cardiode, nefroide y otras.
Los sólidos platónicos
El octaedro es uno de los cinco sólidos platónicos. En esta sección hay infomación de estos poliedros en general.
Otras secciones estudiarán propiedades de cada uno de ellos.
 Presentacion de los sólidos platónicos Presentacion de los sólidos platónicos
Conviene conocerlos y en esta página puedes verlos construidos con diferentes técnicas.
Una vez que los conocemos y nos sabemos sus nombres es interesante contar sus elementos principales. Estos elementos son los vértices, las aristas y las caras.

Presentación de los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro.
 Construcción de sólidos platónicos con pajitas Construcción de sólidos platónicos con pajitas
La propuesta es construir algún sólido platónico con una técnica al alcance de todos. Usaremos pajitas de refresco para las aristas y
las uniremos con limpiapipas (que ahora se pueden comprar en los estancos).

Construcción de los cinco sólidos platónicos con pajitas de refresco. Contamos sus elementos (sus caras, aristas y vértices) y vemos si son rígidos o no.
El tetraedro
En esta sección veremos propiedades del tetraedro.
 Construcción de un tetraedro con un tubo de cartón Construcción de un tetraedro con un tubo de cartón
En la siguiente actividad construiremos un tetraedro un tubo de rollo de papel higiénico gastado.

Construcción de un tetraedro con un rollo de papel higiénico. Esta técnica se usó y todavía se usa para envasar productos.
 Construcción de un tetraedro dentro de un cubo con pajitas Construcción de un tetraedro dentro de un cubo con pajitas
Construcción de un tetraedro inscrito en un cubo hechos con pajitas de refresco:

Una manera muy elegante de dar rigidez al cubo es construir un tetraedro dentro del cubo. A partir de un cubo se pueden construir dos tetradros distintos de este modo.
 Construcción de un octaedro y cuatro tetraedros Construcción de un octaedro y cuatro tetraedros
Construcción de un octaedro y cuatro tetraedros. Obtenemos un tetraedro más grande:

Construcción con pajitas de refresco de un octaedro al que se le añaden cuatro tetraedros para obtener un tetraedro grande.
De estas construcciones podremos sacar interesantes conclusiones matemáticas pues, a partir de ellas, calcularemos el
volumen de un tetraedro de dos modos sencillos.
El octaedro
Construyendo poliedros hacemos objetos muy bonitos que también nos ayudan a comprender sus propiedades matemáticas.
 Construcción de un octaedro de origami Construcción de un octaedro de origami

Construcción de un octaedro con ocho cuadrados de papel. Los seis vértices del octaedro están en 3 cuadrados.
Cálculo mental
Las actividades de cálculo mental son muy indicadas para este nivel.

Ejercicios de cálculo mental en el que se practican algunas estructuras básicas con el propósito de mejorar la seguridad y autoconfianza.
Problemas de la Primavera Matemática
Los problemas sencillos del Concurso de Primavera Matemática son muy indicados para este nivel.

El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
 ANTERIOR ANTERIOR

Página con enlaces de actividades matemáticas que podemos hacer en casa.
MÁS ENLACES

Página con enlaces de actividades matemáticas fáciles que podemos hacer en casa. Pensadas para alumnos de Educación Secundaria, edad aproximada 12-16 años.

Página con enlaces de actividades matemáticas que podemos hacer en casa un poco más complicadas. Pensadas para alumnos de Bachillerato o último año de Educación Secundaria. Edad aproximada, a partir de 15 años.

Ejercicios de cálculo mental en el que se practican algunas estructuras básicas con el propósito de mejorar la seguridad y autoconfianza.

Si tenemos impresora en casa podemos imprimir plantillas en cartulina (o papel) y hacer interesantes construcciones. Muchas son sencillas y puedes intentar hacerlas con reglas y compás. Aunque no puedas hacerlas, también puedes mirarlas pues de ellas sacaremos interesantes consecuencias matemáticas.

El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.

En casa se actualiza, por lo menos, 5 veces a la semana mientras dura el confinamiento. Aquí se puede ver la sucesión cronológica de las publicaciones.

Contacto para dudas, comentarios, enviar fotos con construcciones matemáticas o respuestas.
|


 Magia para adivinar el pensamiento.
Magia para adivinar el pensamiento.
 Plegado y decoración de una piraña de origami.
Plegado y decoración de una piraña de origami.
 Las torres de Hanoi. Versión sobre un cuadro de Magritte.
Las torres de Hanoi. Versión sobre un cuadro de Magritte.
 Rompecabezas del enanito que desaparece.
Rompecabezas del enanito que desaparece.
 Un triángulo que es medido cuadrado.
Un triángulo que es medido cuadrado.

 Todos los cuadrados son semejantes
Todos los cuadrados son semejantes

 Todas las circunferencias son semejantes. El número Pi.
Todas las circunferencias son semejantes. El número Pi.

 Plegado de un cuadrado a partir de un dinA4.
Plegado de un cuadrado a partir de un dinA4.

 Construcción de un cuadrado con pajitas con su diagonal.
Construcción de un cuadrado con pajitas con su diagonal.

 Todas las circunferencias son semejantes. El número Pi.
Todas las circunferencias son semejantes. El número Pi.

 El área de un círculo.
El área de un círculo.
 Circunferencias por dos puntos.
Circunferencias por dos puntos.
 Circunferencias por tres puntos.
Circunferencias por tres puntos.

 No todos los rectángulos son semejantes.
No todos los rectángulos son semejantes.

 Proporción del papel estándar Din A.
Proporción del papel estándar Din A.

 Construcción de una estrellita con una tira de papel
Construcción de una estrellita con una tira de papel





 Presentacion de los sólidos platónicos
Presentacion de los sólidos platónicos
 Construcción de sólidos platónicos con pajitas
Construcción de sólidos platónicos con pajitas

 Construcción de un tetraedro con un tubo de cartón
Construcción de un tetraedro con un tubo de cartón

 Construcción de un tetraedro dentro de un cubo con pajitas
Construcción de un tetraedro dentro de un cubo con pajitas

 Construcción de un octaedro y cuatro tetraedros
Construcción de un octaedro y cuatro tetraedros

 Construcción de un octaedro de origami
Construcción de un octaedro de origami



 ANTERIOR
ANTERIOR