En esta página se presentan actividades matemáticas sencillas pensadas para alumnos de Educación Secundaria.
Se proponen actividades que podemos hacer en casa.
De alguna manera, quiere organizarse por dificultad. Esto no es sencillo. En esta sección encontrarás actividades clasficadas en los siguientes niveles:


Para intentar estas actividades se requiere un poco de conocimiento matemático. Por ejemplo, conocer el Teorema de Pitágoras y poco más.



Cuando se sabe un poco más, por ejemplo, en 3º o 4º de la ESO, estas actividades son un reto.
Iniciamos esta sección con un sencillo truco de magia.

 Las torres de Hanoi. Versión sobre un cuadro de Magritte.
Las torres de Hanoi. Versión sobre un cuadro de Magritte.

 Rompecabezas del enanito que desaparece.
Rompecabezas del enanito que desaparece.

En esta sección vamos a plantear algunas cuestiones referidas a ángulos.


 Doblado de un triángulo equilátero con origami.
Doblado de un triángulo equilátero con origami.



 ¿Cuánto mide el ángulo?
¿Cuánto mide el ángulo?
 Presentacion de los sólidos platónicos
Presentacion de los sólidos platónicos
Conviene conocerlos y en esta página puedes verlos construidos con diferentes técnicas.
Una vez que los conocemos y nos sabemos sus nombres es interesante contar sus elementos principales. Estos elementos son los vértices, las aristas y las caras.

 Los sólidos platónicos y la dualidad
Los sólidos platónicos y la dualidad
Ahora que ya conocemos los sólidos platónicos y hemos contado sus elementos podemos ver que están emparejados. A eso lo llamamos 'dualidad'.
Es un concepto muy sencillo y sorprendente. Además es profundo.

¿Ya conoces las parejas de poliedros regulares? Hay un poliedro regular que no tiene pareja. Decimos que es pareja de él mismo o que es autodual. ¿Sabes cúal es?
En esta sección estudiaremos la semejanza de figuras planas y espaciales.
Es un concepto que usamos en nuestra vida cotidiana y que está relacionada con la escalas (de los planos, mapas, maquetas).
De un modo intuitivo, podemos decir que dos figuras son semejantes si 'tienen la misma forma'.
Luego iremos concretando esta expresión pero resulta que dos figuras semejantes tienen 'sus águlos ccrrespondientes iguales'. Pero además interviene la proporcionalidad y decimos que 'sus lados correspondientes son proporcionales'.
Desarrollaremos más adelante estas ideas con detalle, pero ahora empezamos con un caso concreto, estudiando los cuadrados.

 Cuadrados: lado y diagonal y el lenguaje de las funciones
Cuadrados: lado y diagonal y el lenguaje de las funciones

En esta sección estudiaremos el cuadrado y alguna de sus propiedades, por ejemplo la relación entre el lado la diagonal.

 La diagonal de un cuadrado (1).
La diagonal de un cuadrado (1).


 La diagonal de un cuadrado (2). Usando el lenguaje de las funciones.
La diagonal de un cuadrado (2). Usando el lenguaje de las funciones.

En esta sección vamos a estudiar dos familias de rectángulos especialmente interesantes: los rectángulos raíz cuadrada de 2 y los rectángulos áureos.


 Los rectángulos raíz cuadrada de 2.
Los rectángulos raíz cuadrada de 2.


 Los rectángulos áureos (1).
Los rectángulos áureos (1).
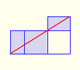


 Los rectángulos áureos (2).
Los rectángulos áureos (2).


 Los rectángulos áureos y la espiral de Durero (3).
Los rectángulos áureos y la espiral de Durero (3).
El pentágono es un polígono muy bonito. Está directamente relacionado con la razón áurea. Es un reto aprender a dibujarlo con regla y compás. Las caras del dodecaedro regular son pentágonos. El pentágono también está relacionado con el icosaedro.


 En casa: El pentágono regular y su diagonal
En casa: El pentágono regular y su diagonal


 En casa: Aprendo a dibujar un pentágono con regla y compás
En casa: Aprendo a dibujar un pentágono con regla y compás
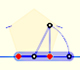
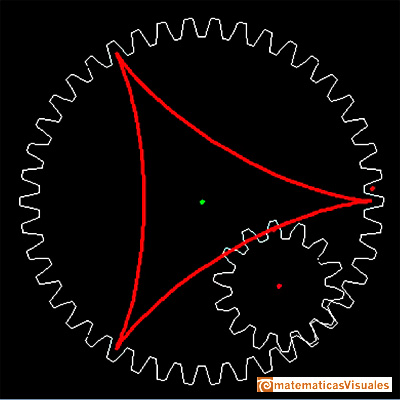
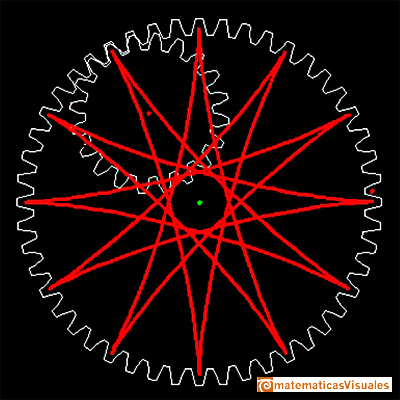
Mostraremos curvas generadas haciendo rodar una circunferencia sobre una recta u otra circunferencia.
Esas curvas se llaman cicloide, hipocicloides y epicicloides.


Se presentan estas curvas con una animación de una transformación continua de la cicloide en una hipocicloide de 3 puntas llamada deltoide.

Veremos propiedades de este poliedro regular que nos resulta tan familiar.


 Sección rómbica de un cubo
Sección rómbica de un cubo
Ya hemos construido un cubo con pajitas de refresco. Ahora vamos a hacer un ejercicio sobre una sección rómbica del cubo.

En esta sección veremos propiedades del tetraedro.

 Construcción de un tetraedro con origami modular
Construcción de un tetraedro con origami modular
Construcción muy bonita de un tetraedro con la técnica de origami modular.

 Cálculos a partir de la construcción de un tetraedro
Cálculos a partir de la construcción de un tetraedro
A partir de la construcción con pajitas de un tetraedro inscrito en un cubo podemos hacer algunos cálculos:


 Cálculo del volumen de un tetraedro (1)
Cálculo del volumen de un tetraedro (1)
Con la misma construcción obtenemos el volumen de un tetraedro.
Construyendo poliedros hacemos objetos muy bonitos que también nos ayudan a comprender sus propiedades matemáticas.


 El volumen de un octaedro
El volumen de un octaedro

En esta sección estudiaremos el icosaedro. Este precioso poliedro es sencillo de construir pues está formado por triángulos equiláteros.

 El icosaedro formado por cuatro rectángulos áureos
El icosaedro formado por cuatro rectángulos áureos

Ejercicios varios sobre áreas y volúmenes de cuerpos geométricos.

 La casita
La casita


 La piscina
La piscina


 El martillo
El martillo
Para las Matemáticas es muy importante demostrar las propiedades. A las importantes las llamamos 'teoremas'.
Algunas de estas demostraciones son muy bonitas y sencillas de seguir. Haciéndolo se aprende mucho sobre lo que de verdad son las Matemáticas.

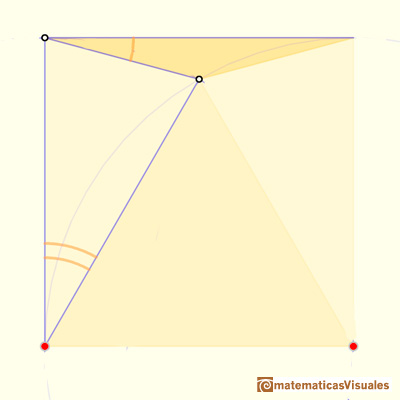
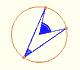
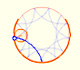
 Circunferencia: propiedad de los angulos inscritos y central
Circunferencia: propiedad de los angulos inscritos y central
Las primeras propiedades se refieren a los ángulos en la circunferencia.
En el siguiente enlace puedes ver una explicación de esas propiedades y después ver las demostraciones.
Hay aplicaciones interactivas que puedes manipular.
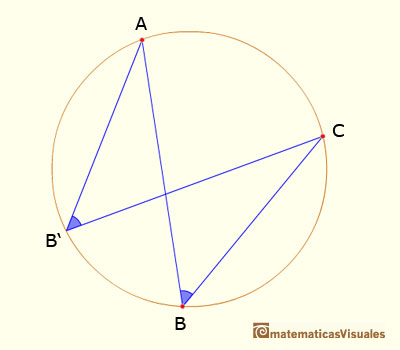
Es interesante ver que para demostrar estas propiedades se descompone la demostración en tres casos más sencillos y, al final, se completa la demostración.
Es una técnica muy habitual a la hora de hacer una demostración. Cada paso te enseña algo diferente y complementario.
La principal propiedad que se usa en esta demostración se refiere a que los triángulos isósceles, los que tienen dos lados iguales, también tienen dos ángulos iguales.

Algunas actividades de cálculo mental son indicadas para este nivel.

Los problemas del Concurso de Primavera Matemática son muy indicados para este nivel.

 ANTERIOR
ANTERIOR
MÁS ENLACES