Triángulos
|
 |
Los tres puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera son los vértices de un triángulo equilátero (Triángulo de Morley).
|
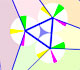 |
Demostración muy bonita y visual de Conway. Podemos jugar con una animación interactiva y ver los diferentes pasos de la demostración.
|
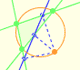 |
A partir de cada punto de la circunferencia circunscrita a un triángulo se obtiene una recta llamada recta de Simson-Wallace o recta de Simson.
|
 |
Demostración interactiva de que los tres puntos que determinan cada recta de Wallace-Simson están alineados.
|
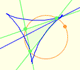 |
La envolvente de las rectas de Simson-Wallace de un triángulo es una curva con tres cúspides que se llama Deltoide de Steiner.
|
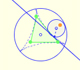 |
La construcción de la deltoide de Steiner como hipocicloide está relacionada con la circunferencia de los nueve puntos.
|
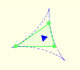 |
El triángulo equilátero determinado por la deltoide de Steiner tiene los lados paralelos al triángulo de Morley pero con orientación opuesta.
|
 |
Demostración dinámica e interactiva del teorema de Pitágoras, inspirada en la de Euclides.
|
 |
Demostración dinámica e interactiva del teorema de Pitágoras por Hermann Baravalle.
|
 |
Podemos ver el teorema de Pitágoras en un mosaico. Es una demostración gráfica sencilla del teorema de Pitágoras que vemos en suelos cuando se combinan cuadrados de dos tamaños.
|
Circunferencias
|
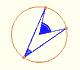 |
Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.
|
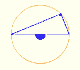 |
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso I: Cuando el arco es una semicircunferencia el ángulo inscrito es recto.
|
 |
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso II: Cuando una cuerda de las que forman el ángulo inscrito es un diámetro.
|
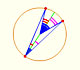 |
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Prueba del caso general.
|
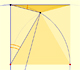 |
Usando regla y compás podemos dibujar ángulos de 15 grados. Son ejemplos básicos de las propiedades de los ángulos central e inscrito en una circunferencia.
|
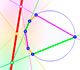 |
Si se inscribe en una circunferencia un hexágono, los puntos de intersección de lados opuestos son colineales.
|
Transformaciones del plano
|
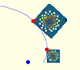 |
Una rotación dilatativa se obtiene combinando una rotación y una dilatación con el mismo centro.
|
 |
Durero estudió transformaciones aplicadas a figuras para, por ejemplo, modificar caras y generar otras caras o caricaturas. Algunas de estas transformaciones son afinidades.
|
 |
Los triángulos equiláteros son figuras semejantes. Si calculamos el área de un solo triángulo equilátero, por semejanza, sabremos el área de cualquier triángulo equilátero. Repasaremos relaciones entre longitudes y áreas de figuras semejantes aplicadas a este caso particular.
|
Espirales
|
 |
En una espiral equiangular el ángulo entre el radio vector y la tangente es constante.
|
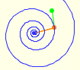 |
Cualquier dilatación de una espiral equiangular tiene el mismo efecto que una rotación.
|
 |
Hay infinitas espirales equiangulares que pasan por dos puntos.
|
Proporción áurea
|
 |
La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.
|
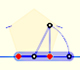 |
Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.
|
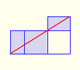 |
A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.
|
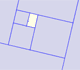 |
Un rectángulo áureo se puede descomponer en un cuadrado y otro rectángulo áureo.
|
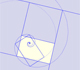 |
Un rectángulo áureo se descompone en un cuadrado y otro rectángulo áureo. Estos rectángulos están relacionados por una rotación dilatativa.
|
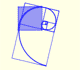 |
La espiral áurea se contruye a partir de rectángulos áureos y es una aproximación simple a una espiral equiangular.
|
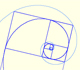 |
Dos espirales equiangulares contienen los vértices de rectángulos áureos.
|
Proporciones
|
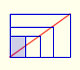 |
El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.
|
Elipses
|
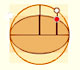 |
Transformando una circunferencia podemos obtener una elipse (como hizo Arquímedes para calcular su área). A partir de la ecuación de la circunferencia deducimos la de la elipse.
|
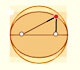 |
Una elipse tiene dos focos y la suma de las distancias de cualquier punto de la elipse a los dos focos es una constante.
|
 |
En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.
|
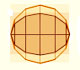 |
En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.
|
 |
El elipsógrafo es un aparato mecánico que se usa para dibujar elipses.
|
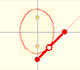 |
Si un segmento de longitud fija se mueve de modo que sus extremos están en dos rectas perpendiculares, cualquier punto del segmento traza una elipse.
|
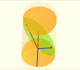 |
La sección de un cilindro por un plano que corta al eje del cilindro en un punto es una elipse. Probamos este resultado usando las esferas de Dandelin.
|
 |
Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.
|
 |
Durero nos mostró un método excelente para dibujar elipses pero cometió un pequeño error. La intuición parece decirnos que la sección de un cono tiene forma de huevo. Podemos probar, usando conceptos básicos, que la elipse tiene dos ejes de simetría.
|
Más curvas
|
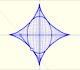 |
La astroide es la envolvente de un segmento de longitud constante cuyos extremos se mueven sobre dos rectas perpendiculares. También es la envolvente de una familia de elipses con la propiedad de que la suma de sus ejes es constante.
|
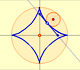 |
La astroide es un caso particular de una familia de curvas que llamamos hipocicloides.
|
Geometría en el espacio
|
 |
Presentación de los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro.
|
 |
Estudiamos el concepto de dualidad de poliedros aplicado a los sólidos platónicos. El cubo y el octaedro son duales, el icosaedro y el dodecaedro son duales y el tetraedro decimos que es autodual.
|
 |
Exposición sobre los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro. Construcción de los poliedros encajados. El Omnipoliedro. Algunas propiedades básicas que se pueden aprender de esta construcción.
|
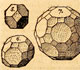 |
Exposición sobre los sólidos arquimedianos realizados por alumnos de 1ºESO del IES Alonso Quijano de Alcalá de Henares.
|
 |
El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.
|
 |
Haciendo adecuadamente secciones en un tetraedro obtenemos rectángulos y, en algún caso, un cuadrado. Podemos calcular el área de esas secciones.
|
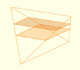 |
En su artículo 'Two Surprising Theorems on Cavallieri Congruence' (Dos teoremas sorprendentes sobre la congruencia de Cavalieri), Howard Eves describe un tetraedro muy interesante. En esta página calculamos las áreas de sus secciones y su volumen.
|
 |
El tetraedro de Howard Eves es congruente Cavalieri con una esfera dada. Podemos ver que las secciones correspondientes tienen áreas iguales. Por lo tanto, el volumen de la esfera es el mismo que el volumen del tetraedro. Sabemos calcular el volumen del tetraedro luego ya sabemos el volumen de la esfera (usando una congruencia sorprendente).
|
 |
Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.
|
 |
Descomponiendo adecuadamente un dodecaedro podemos obtener fácilmente su volumen.
|
 |
El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
|
 |
Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.
|
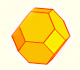 |
El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.
|
 |
El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.
|
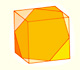 |
Podemos cortar un cubo por la mitad con un plano de modo que la sección sea un hexágono regular. Ocho de estos medios cubos forman un octaedro truncado.
|
 |
Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.
|
 |
El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.
|
 |
El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices
|
 |
El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.
|
 |
El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.
|
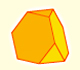 |
El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.
|
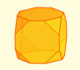 |
Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.
|
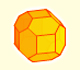 |
Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.
|
 |
Se puede inscribir un cubo en un dodecaedro y podemos ver el dodecaedro como un cubo con seis 'tejados' añadidos uno en cada cara. Estos seis tejados del dodecaedro se pueden plegar en un cubo.
|
 |
Si plegamos los seis tejadillos del dodecaedro dentro de un cubo queda un espacio vacío en el interior. Este espacio es un dodecaedro no regular con todas sus caras pentagonales iguales. Este dodecaedro es un caso particular de piritoedro.
|
 |
Construcción de cinco tetraedros en un dodecaedro con diferentes técnicas: cartulina, origami, tubos, tensegrity. Justificación de esta preciosa construcción.
|
 |
Se pueden colocar cinco tetraedros en un dodecaedro de dos formas distintas, quirales. La combinación de estos dos poliedros da lugar al compuesto de diez tetraedros en un dodecaedro.
|
Geometría del espacio: Esfera
|
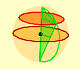 |
Calculamos el área de las secciones de una esfera usando el Teorema de Pitágoras. También estudiamos la relación con la media geométrica o el teorema de la altura de triángulos rectángulos.
|
 |
Estudiamos un tipo de poliedros inscritos en una esfera, en particular la llamada esfera de Campanus que fue muy popular durante el Renacimiento y que Luca Pacioli llamó Septuaginta.
|
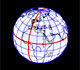 |
Un mapa básico de la Tierra como una esfera. Sistema de Coordenadas Geográfico: Latitud, longitud.
|
 |
Esta proyección tiene la propiedad de preservar el área. El área de la esfera es igual al área lateral del cilindro circunscrito. Conociendo el área de la esfera podemos deducir su volumen, tal como hizo Arquímedes.
|
Geometría en el espacio: Dodecaedro rómbico
|
 |
La Humanidad ha estdo siempre fascinada por cómo las abejas construyen sus panales. Kepler relacionó la forma de los panales con un poliedro que llamamos dodecaedro rómbico.
|
 |
Queremos cerrar un prisma hexagonal como lo hacen las abejas, usando tres rombos iguales. ¿Qué forma deben tener estos tres rombos para cerrar el prisma con la menor superficie?
|
 |
Añadiendo seis pirámides a un cubo podemos construir nuevos poliedros que tienen veinticuatro caras triángulares. Para unas determinadas pirámides obtenemos un dodecaedro rómbico que tiene doce caras rómbicas.
|
 |
Podemos construir un dodecaedro rómbico añadiendo seis pirámides a un cubo. Este hecho tiene interesantes consecuencias.
|
 |
Podemos llenar el espacio con dodecaedros rómbicos sin dejar huecos.
|
 |
Una cadena de seis pirámides puede plegarse hacia dentro y formar un cubo y puede plegarse hacia fuera y colocarse sobre otro cubo y formar un dodecaedro rómbico.
|
 |
Kepler relaciona el dodecaedro rómbico con el apilamiento de balas de cañón. Si se comprime un determinado apilamiento, las balas se deforman en este poliedro.
|
 |
El ángulo obtuso de las caras rómbicas del dodecaedro rómbico se conoce como ángulo de Maraldi. Solo se necesita un poco de trigonometría básica parar calcularlo.
|
 |
A partir de un conocimiento básico del dodecaedro rómbico se puede calcular rápidamente la densidad del empaquetamiento óptimo de esferas.
|
 |
Tetraxis es un puzle muy interesante, sencillo y bonito, diseñado por Jane y John Kostick. Estudiaremos algunas propiedades de este juego y su relación con el dodecaedro rómbico. Plantillas para construir un Tetraxis con cartulina e imanes. El rompecabezas hecho con impresión 3D.
|
Geometría en el espacio: Rombicuboctaedro y pseudo rombicuboctaedro
|
 |
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro.
|
 |
También llamado girobicúpula cuadrada elongada. Es muy parecido al rombicuboctaedro pero es menos simétrico.
|
 |
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro aumentado.
|
 |
En esta segunda versión del rombicuboctaedro aumentado podemos separar las pirámides y ver el interior de la figura. Luca Pacioli escribió que 'podemos ver el interior solo con nuestra imaginación'. La aplicación interactiva solo nos ayuda a ello.
|
 |
A partir de un rombicuboctaedro podemos añadir pirámides a sus caras. Obtenemos un precioso poliedro que parece una estrella.
|
Desarrollos planos de cuerpos geométricos
|
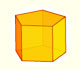 |
Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.
|
 |
Prismas con base regular o irregular cortados por un plano no paralelo a la base y sus desarrollos planos.
|
 |
Los cilindros son superficies de revolución que pueden desarrollarse en un plano. Se explica cómo calcular la superficie lateral y total de un cilindro.
|
 |
La sección de un cilindro por un plano es una elipse. Estas figuras se llaman segmentos cilíndricos o cilindros truncados y pueden desarrollarse en el plano.
|
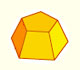 |
Desarrollos planos de pirámides y de troncos de pirámide de base regular con diferentes números de lados.
|
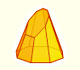 |
Desarrollos planos de pirámides truncadas por un plano oblicuo.
|
 |
Desarrollos planos de conos y troncos de cono. Cálculo del área lateral de estas figuras.
|
 |
Desarrollos planos de conos truncados por un plano oblicuo. La sección es una elipse.
|
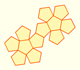 |
El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
|
 |
El primer dibujo del desarrollo plano del octaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
|
 |
El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
|
Construcción de poliedros. Técnicas sencillas
|
 |
Breve introducción a una serie de páginas sobre técnicas sencillas de construcción de poliedros. Un poco de historia.
|
 |
Podemos dibujar los desarrollos planos en cartulina y construir poliedros uniendo solapas con pegamento.
|
 |
Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.
|
 |
Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.
|
 |
Técnica simple para construir poliedros pegando discos de cartulina.
|
 |
El diseñador italiano Bruno Munari pensó 'Acona Biconbi' como un trabajo de escultura. También es un juego de construcción con el que podemos jugar con colores y formas.
|
 |
Con tres rectángulos áureos podemos construir un icosaedro.
|
 |
El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.
|
 |
Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.
|
 |
Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.
|
 |
Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.
|
 |
Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.
|
 |
Material para la sesión del TTM (Zaragoza, 8 de marzo de 2024). Con plantillas para descargar y construir dodecaedros rómbicos y celdas de abejas.
|
 |
Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.
|
 |
Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.
|
 |
Material para la sesión del TTM (Zaragoza, el 10 de marzo de 2023). Con plantillas para descargar y construir varias figuras geométricas.
|
 |
Microarquitectura es un juego de construcción desarrollado por Sara San Gregorio. Podemos jugar con él y construir muchas estructuras inspiradas en poliedros.
|
 |
Material para la sesión del TTM (Zaragoza, el 20 de Octubre de 2017). El objetivo principal es disfrutar con las Matemáticas y fomentar la construcción de poliedros por su valor estético y también porque nos facilitan la comprensión de resultados matemáticos.
|
 |
Material para la sesión del TTM (Zaragoza, el 19 de Octubre de 2018). Diferentes construcciones del icosaedro nos ayudan a comprender sus propiedades. El objetivo principal es disfrutan construyendo poliedros.
|
 |
Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.
|
 |
Un icosaedro se puede poner dentro de un octaedro de modo que sus 12 vértices estén en las 12 aristas del octaedro. Dos construcciones nos ayudan a comprender esta relación y, gracias a ella, calcularemos el volumen del icosaedro.
|
 |
Kepler relaciona el dodecaedro rómbico con el apilamiento de balas de cañón. Si se comprime un determinado apilamiento, las balas se deforman en este poliedro.
|
 |
Construcción de un pequeño dodecaedro estrellado como metáfora del confinamiento que estamos viviendo por la pandemia del coronavirus COVID-19.
|
Construcción de poliedros. Impresión 3d
|
 |
Construcción del tetraedro con impresión 3d. El tetraedro es un poliedro autodual. El centro del tetraedro.
|
 |
Construcción del cubo y del octaedro con impresión 3D. El cubo y el octaedro son poliedros duales.
|
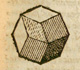 |
Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.
|
Mecanismos
|
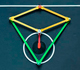 |
Presentación de algunos mecanismos articulados y su relación con las Matemáticas. Modelos realizados con materiales sencillos, impresión 3D. Algunos modelos motorizados y controlados con Arduino.
|
