Este tipo de poliedros que están inscritos en una esfera era bien conocido por Euclides. En la proposición 17 del libro XII de los Elementos, Euclides muestra la construcción de un poliedro entre dos esferas concéntricas.
Durante la Edad Media, Campanus de Novara (1220-1296) escribió una versión de los Elmentos de Euclides que fue muy difundida. Campanus usó la construcción de Euclides para describir un poliedro de 72 caras. Este poliedro fue muy popular durante el Renacimiento y se conoció como esfera de Campanus.
Leonardo da Vinci dibujó este poliedro para el libro de Luca Pacioli 'De Divina Proportione' (La divina proporción). Allí recibe el nombre de Septuaginta.

He tenido curiosidad por saber de donde viene el usar 'septuaginta' para designar este poliedro pues septuaginta significa setenta en latín (y no setenta y dos). Septuaginta es el nombre que recibe la primera traducción de las Escrituras hebreas en griego y querría decir 'de los setenta'. Pero la tradición dice que fueron 72 sabios judios los que participaron en esa traducción, seis por cada una de las doce tribus de Israel.
Usando la aplicación interactiva de esta página podemos obtener imágenes como éstas:

Si añadimos más y más caras, este poliedro es más y más parecido a un esfera:


Una manera de construir un poliedro inscrito en una esfera es la siguiente:
Consideremos una esfera y sean N y S los polos Norte y Sur de esa esfera y sea C la circunferencia del ecuador. Inscribimos en C un polígono regular con un número de aristas que sea múltiplo de 4, sea 4n. Construyamos 2n polígonos de 4n aristas de modo que tengan un vértice en N, otro en S y dos vértices en dos vértices opuestos del polígono ecuatorial. Estos polígonos serían semejantes a las líneas de longitud. Después unimos los vértices de estos polígonos con 'líneas de latitud'. El resultado es un polígono con 8n^2 caras.
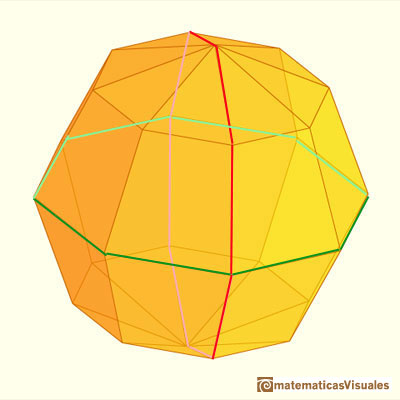
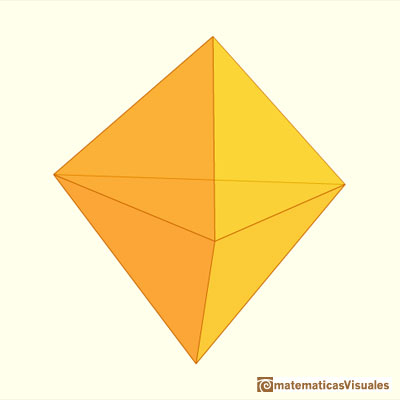
Si n=1 el resultado es el octaedro (con sus 8 caras):
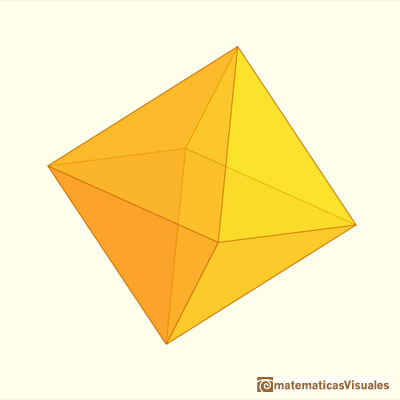

Si n=2 obtenemos un poliedro con 32 caras:



Si n=3 el poliedro tiene 72 caras y éste es el que era conocido como esfera de Campanus y que Luca Pacioli llamó Septuaginta.



La aplicación interactiva es más flexible y con ella podemos dibujar poliedros de modo que el polígono ecuatorial tenga un número par o impar de aristas y que los 'polígonos de longitud' tengan un número de aristas distinto del polígono ecuatorial. Si el polígono ecuatorial tiene un número impar de vértices entonces las líneas de longitud van del polo N al S pero no se cierran.


REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES