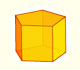
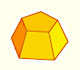
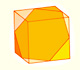
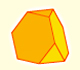
A cuboctahedron is an Archimedean solid.
It is generated by truncating the vertices of a cube or of an octahedron at 1/2 edge-length.
There are 6 square faces on the cuboctahedron, one for each face of the cube. There are 8 equilateral triangular faces, one for each vertex of the cube.
We are going to calculate the volume of an octahedron of edge-length 1 starting from the volume of a cube.
If a cuboctahedron has edge-length 1, the cube that contains it is:
The volume of this cube is:
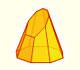
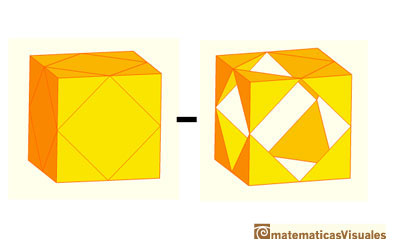
To calculate the volume of a cuboctahedron we have to subtract from the volume of the cube the volume of the 8 pyramids that we cut off.
The volume of each of these 8 pyramids is:
Now, we can calculate the volume of the cuboctahedron (what we subtract, 8 pyramids, may be reasssembled into an octahedron of edge-length 1)
Then the volume of a cuboctahedron of edge-length a is:
Now we are going to see one interesting property of the cuboctahedron. If we think in this cube as made for eight small cubes (with the center of the cube as a vertex shared by the small cubes)
we can see that the distance from the center of the cuboctahedron (its center of gravity) to any vertex is the edge length (it is equal
to a diagonal of a side of one small cube).
Then a cuboctahedron is made of six half octahedra and eight tetrahedra, all of these pyramids sharing one vertex in the center of gravity of the cuboctahedron.
The cuboctahedron is the only spatial configuration in wich the length of each polyhedral edge is equal to that the distance from
its center of gravity to any vertex.
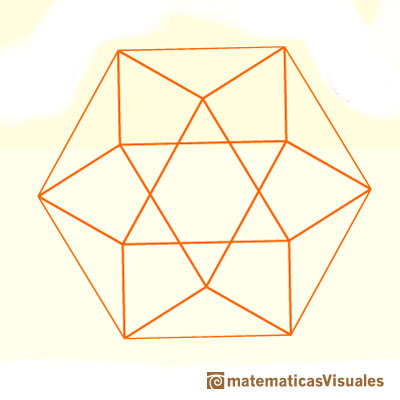
More than that, its 24 edges lies in four hexagons centered in the center of gravity of the cuboctahedron.
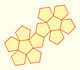
In this origami cuboctahedron, can you see the hexagon (paralel to the floor)?
I made this origami cuboctahdron following the instructions in Tomoko Fusè's book 'Unit Origami' (Japan Publications, Inc. 1990)
Can you see here four hexagons?
Vertices of this beautiful modular origami model, the Omega Star, are vertices of a cuboctahedron:
One interesting property of the cuboctahedron is that the distance from the solid's center to each vertice is equal to its edge length:
A cuboctahedron on a wall in Rothenburg ob der Tauber (Germany, 2013)
A cuboctahedron on a door in the Schottenkirche St. Jakob (Scots Church of St. James) in Regensburg (Germany, 2014)
Cuboctahedrons in the Schöner Brunnen (The Beautiful Fountain) in Nuremberg (Germany, 2014).
In he Beautiful Fountain you can see several images of scientis of the Antiquity:
Schöner Brunnen (The Beautiful Fountain) in Nuremberg (Germany, 2014, RCR)
Pythagoras in Schöner Brunnen (The Beautiful Fountain) in Nuremberg (Germany, 2014, RCR)
Euclid in Schöner Brunnen (The Beautiful Fountain) in Nuremberg (Germany, 2014, RCR)
Ptolemy in Schöner Brunnen (The Beautiful Fountain) in Nuremberg (Germany, 2014, RCR)
There are several polyhedra (cuboctahedron, icosidodecahedron and more) in some intarsia panels in El Escorial (Madrid, Spain).
I think that this intarsia panels are not very well known
although Cromwell wrote: "There are also examples of polyhedra in the royal palace at El Escorial just outside Madrid.
The palace was erected by Philip II (1527-1598), who is said to have excelled in mathematical studies as a young prince.
The doors to the throne-room at the palace were a gift from his father-in-law, Maximilian II. They were ornately carved and
inlaid b German craftsmen. The intarsia panels contain some of the typical elements (lutes, books) and some polyhedra".
(Cromwell, p. 117)
REFERENCES
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition (p. 197)
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961 (p. 87).
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
Luca Pacioli - De divina proportione - (La divina proporción) Ediciones Akal, 4ª edición, 2004. Spanish translation by Juan Calatrava.
Mª Paz Aguiló, La ebanistería alemana en el Monasterio de El Escorial.
MORE LINKS

The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.

The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.

The volume of a tetrahedron is one third of the prism that contains it.

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.

Plane nets of prisms with a regular base with different side number cut by an oblique plane.

We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.

We study different cylinders cut by an oblique plane. The section that we get is an ellipse.
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.
Plane net of pyramids cut by an oblique plane.

Plane developments of cones and conical frustum. How to calculate the lateral surface area.

Plane developments of cones cut by an oblique plane. The section is an ellipse.
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.

The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
We can cut in half a cube by a plane and get a section that is a regular hexagon. Using eight of this pieces we can made a truncated octahedron.

Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.

These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.

The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).

Modular Origami is a nice technique to build polyhedra.
The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.
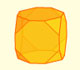
When you truncate a cube you get a truncated cube and a cuboctahedron. If you truncate an octahedron you get a truncated octahedron and a cuboctahedron.

You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.






















 NEXT
NEXT
 PREVIOUS
PREVIOUS










































