We can see Pythagoras' Theorem in a tiling. It is a graphic demonstration of Pythagoras' Theorem we can see in some floor made using squares of two different sizes.

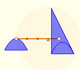Archimedes show us in 'The Method' how to use the lever law to discover the area of a parabolic segment.

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.

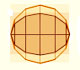In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated tetrahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the rhombicuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the Campanus' sphere.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the augmented rhombicuboctahedron.

We can see the interior of the augmented rhombicuboctahedron. Luca Pacioli wrote that you 'can see the interior only with your imagination'.

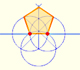In his book 'Underweysung der Messung' Durer draw a non-regular pentagon with ruler and a fixed compass. It is a simple construction and a very good approximation of a regular pentagon.

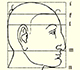He studied transformations of images, for example, faces.

Durer was the first who published in german a method to draw ellipses as cone sections.

Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.

Kepler was one mathematician who contributed to the origin of integral calculus. He used infinitesimal techniques for calculating areas and volumes.

Studying the volume of a barrel, Kepler solved a problem about maxima in 1615.

Kepler was one mathematician who contributed to the origin of integral calculus. He used infinitesimal techniques for calculating areas and volumes. In this page we study one optimization problem.

Using Cavalieri's Principle we can calculate the volume of a sphere.

Mercator published his famous series for the Logarithm Function in 1668. Euler discovered a practical series to calculate.