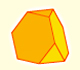
|
|
|
Octahedron (adapted from Leonardo da Vinci)
This video is an adaptation of the drawing that Leonardo da Vinci made of the octahedron (Octocedron planus vacuus) for Luca Pacioli's book 'De Divina Proportione'.
Pacioli wrote about the octahedron (Spanish translation):
"El octaedro plano hueco o sólido tiene doce líneas, veinticuatro ángulos superficiales y seis sólidos y está contenido
por ocho bases triangulares equiláteras y equiángulas, como se nos presenta en su propia forma material."
('La divina proporción' de Luca Pacioli, page 93, Spanish translation by Juan Calatrava, Editorial Akal, 4th edition, 2008)
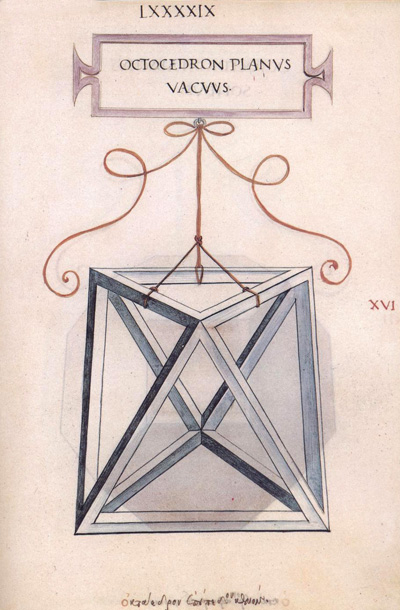
Leonardo da Vinci's drawing of the octahedron (Octocedron planus vacuus) for Luca Pacioli's book 'De divina proportione'. (There is an Spanish version, 'La divina proporción' Editorial Akal. Image used with permission of Editorial Akal).
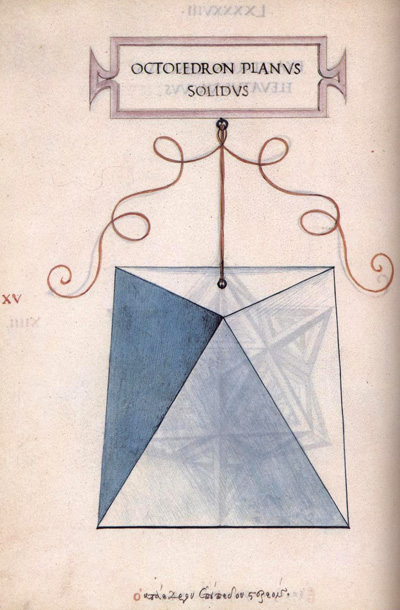
Leonardo da Vinci's drawing of the octahedron (Octocedron planus solidus) for Luca Pacioli's book 'De divina proportione'. (There is an Spanish version, 'La divina proporción' Editorial Akal. Image used with permission of Editorial Akal).
If you play with the interactive application you can get images like these:
REFERENCES
Luca Pacioli - La divina proporción - Ediciones Akal, 4th edition, 2004. Spanish edition of 'De divina proportione'. Translation by Juan Calatrava.
Leonardo da Vinci's Geometric Sketches Frank J. Swetz's article in MathDl, Loci:Convergence.
Leonardo da Vinci's Polyhedra George Hart's excellent website about polyhedra.
NEXT
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the rhombicuboctahedron.
PREVIOUS
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated tetrahedron.
MORE LINKS
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the Campanus' sphere.
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.
The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.
The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.
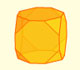
When you truncate a cube you get a truncated cube and a cuboctahedron. If you truncate an octahedron you get a truncated octahedron and a cuboctahedron.
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.