It is a very interesting experience to build and touch a model of an octahedron.
We can use cardboard (the octahedron consists of eight equilateral triangles):
Very basic origami (the six vertices are in three squares in three orthogonal planes):
Or you can use twelve plastic tubes:
An octahedron is composed by two pyramids of square base.
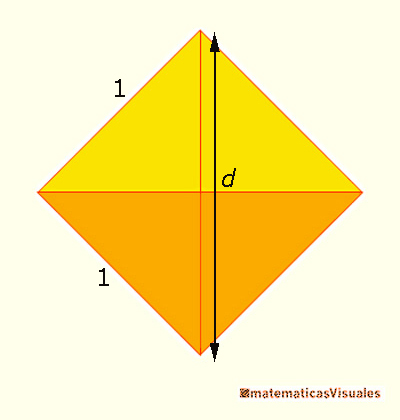
We can see the height of these two pyramides as the diagonal of a square.
The diagonal of a square of edge length 1 is:
Therefore, the volume of an octahedron of edge length 1 is (remember that the volume of a pyramid is one third of the base area times the perpendicular height):
And the volume of an octahedron of edge length a is:
Using that we can calculate the volume of a tetrahedron.
We can consider a tetrahedron of edge length 2:
We can write a relation:
A tetrahedron of edge length 2 is made of one octahedron and four tetrahedra of edge length 1:
Then, the volume of an octahedron is four times the volume of a tetrahedron and we can recalculate the
volume of a tetrahedron.
REFERENCES
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition (p. 197)
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961 (p. 87).
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
Luca Pacioli - De divina proportione - (La divina proporción) Ediciones Akal, 4ª edición, 2004. Spanish translation by Juan Calatrava.
MORE LINKS

The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Demonstration of Pythagoras Theorem inspired in Euclid.

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.

These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.

The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.

Using cardboard you can draw plane nets and build polyhedra.

A very simple technique to build complex and colorful polyhedra.

Using cardboard you can build beautiful polyhedra cutting polygons and glue them toghether. This is a very simple and effective technique. You can download several templates. Then print, cut and glue: very easy!

Examples of polyhedra built using tubes.

Modular Origami is a nice technique to build polyhedra.

Examples of polyhedra built using tensegrity.

Examples of polyhedra built using Zome.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.

We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.

Plane developments of cones and conical frustum. How to calculate the lateral surface area.
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.










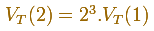


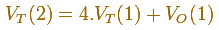


 NEXT
NEXT





























 PREVIOUS
PREVIOUS












