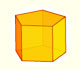
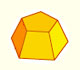
A regular dodecahedron is a polyhedron with twelve regular pentagonal faces. It is a Platonic solid well known from Antiquity.

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
Leonardo da Vinci drew two dodecahedra for Luca Pacioli's book 'De Divina Proportione' (published in 1509).

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.
It was Durer the first to publish plane nets of polyhedra. In his
book 'Underweysung der Messung' ('Four Books of Measurement', published in 1525) the author draw plane developments of several
Platonic and Archimedean solids, for example, this regular dodecahedron:
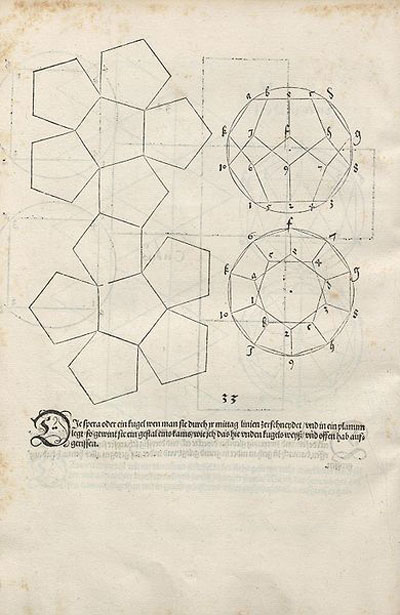
"Whether or not Dürer was acquainted with the work of the two Italian specialists in this fiel, Luca Pacioli
and Piero della Francesca, is an open question. Certain it is that (...) he tackled the problem in an entirely independent way. Pacioli
(...) illustrates them [several polyhedra] in perspective or stereographic images. Dürer treats (...)[more polyhedra] and instead of
representing the solids in perspective or stereographic images, he devised the apparently original and, if one may say so,
proto-topological method of developing them on the plane surface in such a way that the facets form a coherent 'net' which,
when cut out of paper and properly folded where two facets adjoin, will form an actual, three-dimensional model of the solid
in question." (Panofsky, p.259)
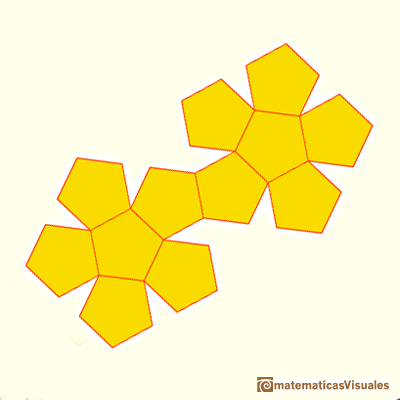
You can draw the plane net of a dodecahedron drawing twelve regular pentagons with ruler and compass:
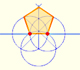
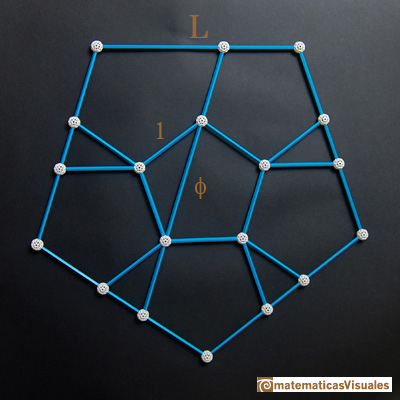
You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.
Six regular pentagons make a big pentagon. It is easy to calculate its side length if you remember some properties of
the golden ratio, deeply related with
the regular pentagon:

The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.
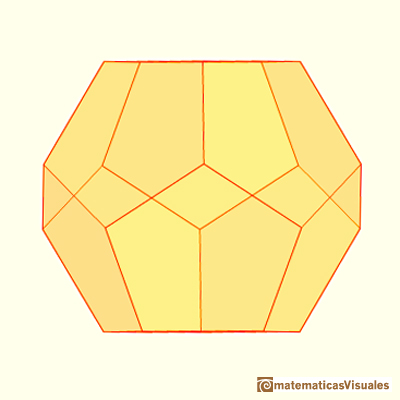
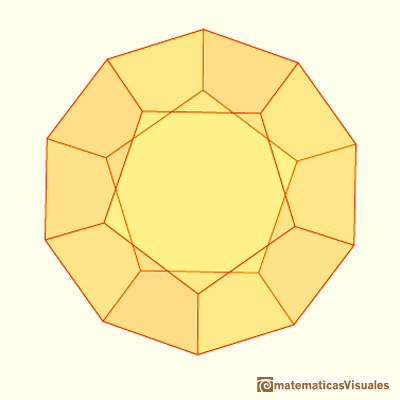
Developing a dodecahedron:
Playing with projections as Durer did:
It is a pleasure to build your own dodecahedron with construction paper:
You can download the plane net of this dodecahedron (and much more) in
Furuti's page about Map Projections.
You can build a dodecahedron with rubber bands and construction paper.
If you want to learn how to build this polyhedron or to download templates go to Resources: how to build polyhedra with paper and rubber bands.
I learned the following construction from Steinhaus' book 'Mathematical Snapshots':
[Look at the table, its shape is an hyperellipse I made with oak]
REFERENCES
Erwin Panofsky - The Life and Art of Albrecht Dürer - Princeton University Press
Dan Pedoe - Geometry and the Liberal Arts - St. Martin's Press (p. 76)
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition (p. 197)
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961 (p. 87).
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
MORE LINKS

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.

If you fold the six roofs of a regular dodecahedron into a cube there is an empty space. This space can be filled with an irregular dodecahedron composed of identical irregular pentagons (a kind of pyritohedron).

The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.

You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.
In his book 'Underweysung der Messung' Durer draw a non-regular pentagon with ruler and a fixed compass. It is a simple construction and a very good approximation of a regular pentagon.

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron
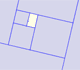
A golden rectangle is made of an square and another golden rectangle.
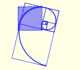
The golden spiral is a good approximation of an equiangular spiral.
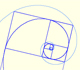
Two equiangular spirals contains all vertices of golden rectangles.
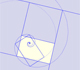
A golden rectangle is made of an square an another golden rectangle. These rectangles are related through an dilative rotation.
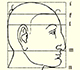
He studied transformations of images, for example, faces.

One eighth of a regular dodecahedon of edge 2 has the same volume as a dodecahedron of edge 1.
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.

We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.

Plane developments of cones and conical frustum. How to calculate the lateral surface area.

The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The volume of a tetrahedron is one third of the prism that contains it.

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
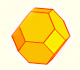
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.

The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.
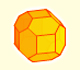
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).











 NEXT
NEXT
 PREVIOUS
PREVIOUS












































