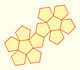
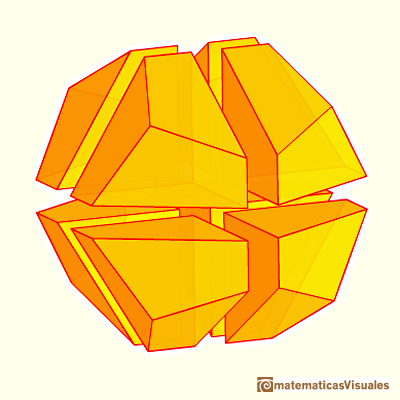
One eighth of a dodecahedron of side length 2 has the same volume of a dodecahedron of side length 1.
We are going to study the volume of a dodecahedron looking at this figure.
We can decompose one eight of a
dodecahedron of side length 2 in several pieces and calculate the volume of these pieces.
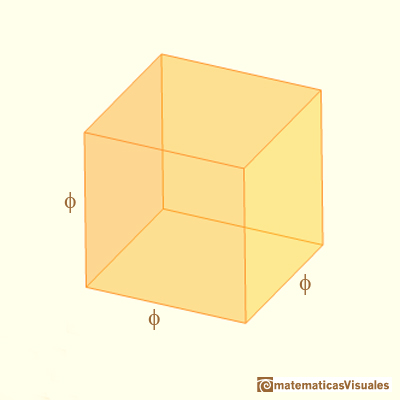
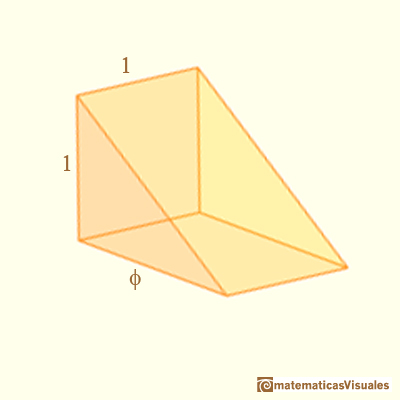
There are one cube, three wedges and three pyramids:
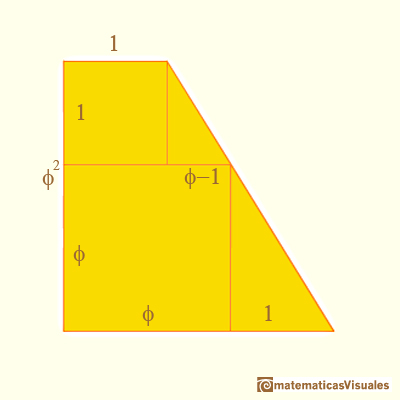
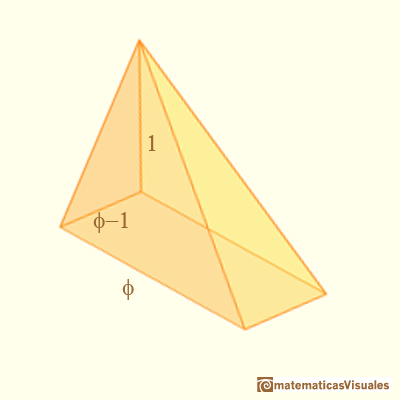
These are important measures in this figure, related with the golden section:
Remember that
There is one cube and its volume is:
There are three wedges and the volume of one wedge is:
There are three pyramids and the volumen of a pyramid is:
Then the volume of a dodecahedron of side length 1 is:
The volume of a dodecahedron of side length a is:
Some minerals, like pyrite, cristalize in dodecahedra (non-regular, it is sometimes called pyritohedron)
MORE LINKS

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

A Cube can be inscribed in a Dodecahedron. A Dodecahedron can be seen as a cube with six 'roofs'. You can fold a dodecahedron into a cube.

If you fold the six roofs of a regular dodecahedron into a cube there is an empty space. This space can be filled with an irregular dodecahedron composed of identical irregular pentagons (a kind of pyritohedron).

The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.
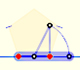
You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.
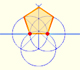
In his book 'Underweysung der Messung' Durer draw a non-regular pentagon with ruler and a fixed compass. It is a simple construction and a very good approximation of a regular pentagon.

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron
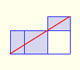
From Euclid's definition of the division of a segment into its extreme and mean ratio we introduce a property of golden rectangles and we deduce the equation and the value of the golden ratio.
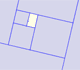
A golden rectangle is made of an square and another golden rectangle.
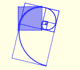
The golden spiral is a good approximation of an equiangular spiral.
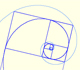
Two equiangular spirals contains all vertices of golden rectangles.
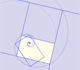
A golden rectangle is made of an square an another golden rectangle. These rectangles are related through an dilative rotation.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).

The volume of a tetrahedron is one third of the prism that contains it.

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.

The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.

The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.

You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.








 NEXT
NEXT
 PREVIOUS
PREVIOUS