An icosahedron is a platonic solid. Its faces, like the thetrahedron and the octahedron, are equilateral triangles.
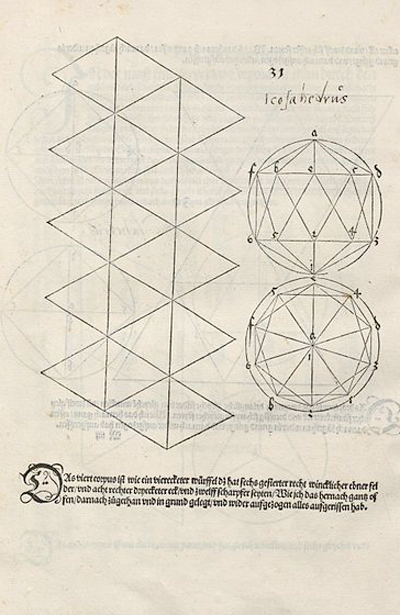
It is very easy to build one using its plane net, as Dürer taught us in his book 'Underweysung der Messung' ('Four Books on Measurement') published in 1525:
Or we can make this beautiful lamp:

In this page we are going to study the relation between the golden ratio and the icosahedron.
The golden rectangle is a beautiful construction also related with some spirals and the dodecahedron.
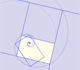
We can put three golden rectangles (in three mutually orthogonal planes) and make a well known construction. These rectangles have 12 vertices. The distance between any pair of neighbouring points is equal to the short side of one golden rectangle. Then, these 12 points coincide with the 12 vertices of an icosahedron.

By symmetry, these twelve triangles are isosceles triangles but, they are equilateral?

One easy way to convince yourself about that is calculating the height of one of these triangles:

Remember that
Then
And h is the height of a equilateral triangle of side length 2:
Three planes contains the 20 vertices of an icosahedron. Their edges form Borromean rings.
You can made the Borromean rings using three balloons. This constrution is inspired in a video about the logo of the International Mathematical Union (IMU) designed by John Sullivan (The Borromean Rings: a new logo for the IMU).

We are going to calculate the volumen of an icosahedron of side length 2:
An icosahedron has twenty equilateral triangles.
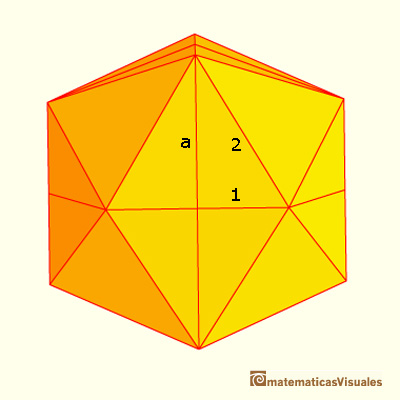
The area of one of the twenty equilateral triangles that the icosahedron of side 2 have is:
The volume of an icosahedron of side 1 is one eigth of the volume of an icosahedron of side 2.
The volume of the icosahedron of side 1 is the same as the volume of two and a half pyramids. We need to calculate the height of one of this pyramids: the distance between the center and one triangular face.
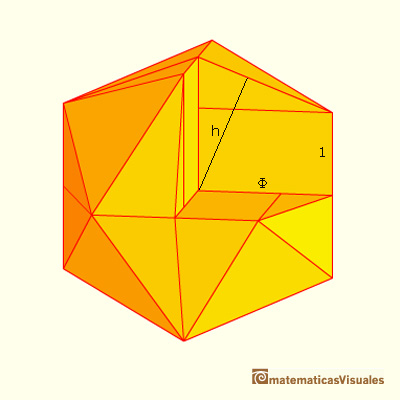
There are two similar triangles and we can write:
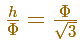
Then the volume of one pyramid is:
And the volume of an icosahedron of side 1 is:

The six vertices of an octahedron lies in three mutually ortogonal squares. We can put inside each square a golden rectangle (for example, using tubes):

The same construction with Zome:

Then, if the twelve edges of an octahedron are divided in the golden ratio (in some order) these vertices are the vertices of an icosahedron.

It is not difficult to calculate the volume of the octahedron and the volume of the six bipyramids and get the volume of the icosahadron.

Icosahedron and octahedron, one inside each other, with Zome: .
An icosahedron, an octahedron and a tetrahedron, one inside each other, made using using tubes:
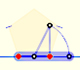
We can build the structure of an icosahedron using six sticks and six elastic bands. It is one of the simplest examples of using "tensegrity".



REFERENCES
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS