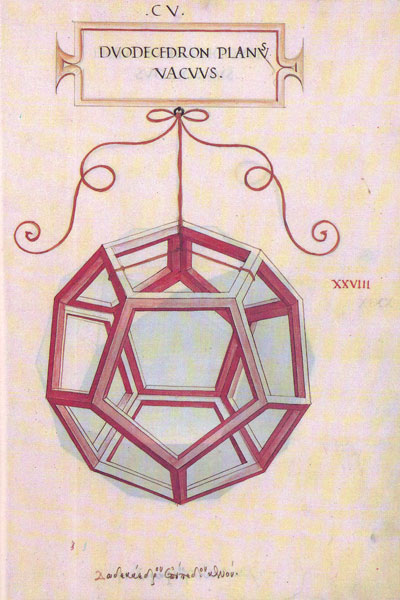
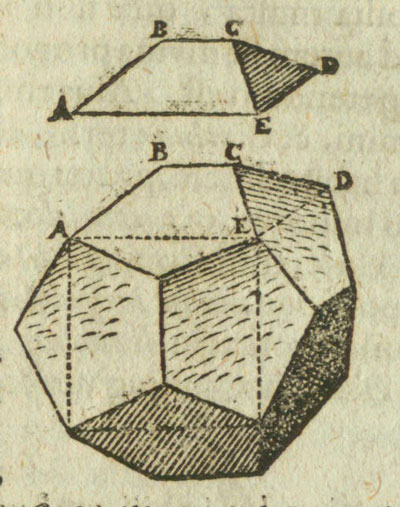
Leonardo da Vinci drew two dodecahedra for Luca Pacioli's book 'The Divine Proportione'.
Kepler was interested in this wonderful geometric body (For example, you can see this drawing in his book
'Hamonices Mundi - The Harmony of the World', (1619)
(Read the original book at Posner Memorial Collection):
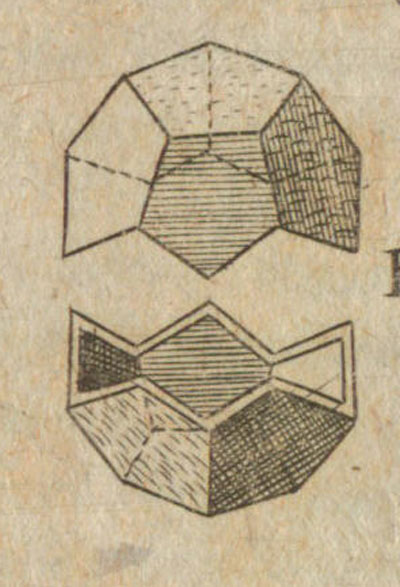
In Dürer's book 'Underweysung der Messung' the author published the first plane net of a regular dodecahedron.
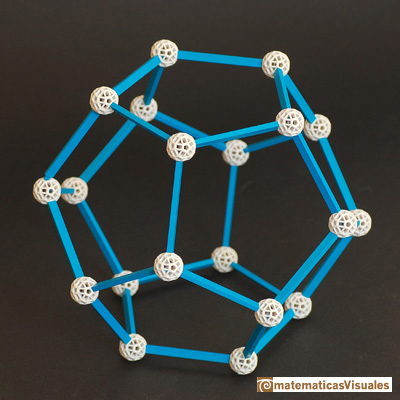
A regular dodecahedron is a platonic polyhedron made by 12 regular pentagons.
Then there is a deep relation between the dodecahedron and the golden ratio.
Points of coordinates:
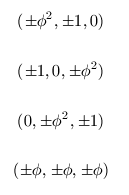
are the 20 vertices of a regular dodecahedron of edge 2.
Where 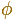 is the golden ratio we've seen in the golden rectangle.
is the golden ratio we've seen in the golden rectangle.
We can calculate the distance between pairs of adjacents vertices to convince ourselves.
We can build this figure using Zome:
Kepler showed us how to put a cube inside a regular dodecahedron:
A cube can be inscribed in a dodecahedron so that each edge of the cube lies in a face of the dodecahedron and joins two alternate vertices
of that face. (Ball and Coxeter, p. 131)
A regular dodecahedron can be inscribed into an sphere. To calculate the radius of this sphere we can think that its center is the center of the cube,
and the cube has side length equal to phi if the side lenght of the dodecahedron is 1. Or you can see this figure. Then
To calculate the volume of a dodecahedron, notice that the volume of a dodecahedron of side length 1 is one eighth the volume of a dodecahedron of side length 2,
it is to say, this body:
With the help of Zome we can study the volume of a regular dodecahedron.
Origami: building a dodecahedron with the Tom Hull's PHiZZ module:
Origami: building a dodecahedron with the penultimate module (learn more about the penultimate module):
Dodecahedron and icosahedron are dual polyhedra.
You can build a dodecahedron and an icosahedron with corresponding edges perpendicularly bisecting each other. Then, the common part
is an icosidodecahedron. (Ball and Coxeter, 136)
If you want to learn how to build this polyhedron or to download templates go to Resources: how to build polyhedra with paper and rubber bands.
Icosidodecahedron with twenty triangular faces and twelve pentagonal faces it is a toy for your pet:
Vertices of the dodecahedron (20) and vertices of the icosahedron (12) are the vertices of a rhombic triacontahedron:
Triacontahedron and icosidodecahedron are dual polyhedra just as the dodecahedron and the icosahedron are dual polyhedra.
Five tetrahedra inside a dodecahedron. One of the most wonderful constructions I have ever made. The first time I read about this construction was
in Magnus J. Wenninger's book 'Polyhedron models for the classroom' and I made this model more than twenty years ago.
You can download a template from
Korthalsates site.
Origami: Five tetrahedra inside a dodecahedron. See instructions on how to buil this origami model:
Zome: Five tetrahedra inside a dodecahedron:
The side length of the tetrahedron inside a dodecahedron of side length 1 is:
Tubes: Five tetrahedra inside a dodecahedron:
REFERENCES
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
MORE LINKS
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

A Cube can be inscribed in a Dodecahedron. A Dodecahedron can be seen as a cube with six 'roofs'. You can fold a dodecahedron into a cube.

If you fold the six roofs of a regular dodecahedron into a cube there is an empty space. This space can be filled with an irregular dodecahedron composed of identical irregular pentagons (a kind of pyritohedron).

The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.
You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.
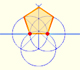
In his book 'Underweysung der Messung' Durer draw a non-regular pentagon with ruler and a fixed compass. It is a simple construction and a very good approximation of a regular pentagon.

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron
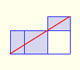
From Euclid's definition of the division of a segment into its extreme and mean ratio we introduce a property of golden rectangles and we deduce the equation and the value of the golden ratio.
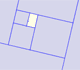
A golden rectangle is made of an square and another golden rectangle.
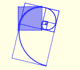
The golden spiral is a good approximation of an equiangular spiral.
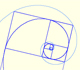
Two equiangular spirals contains all vertices of golden rectangles.
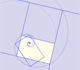
A golden rectangle is made of an square an another golden rectangle. These rectangles are related through an dilative rotation.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).

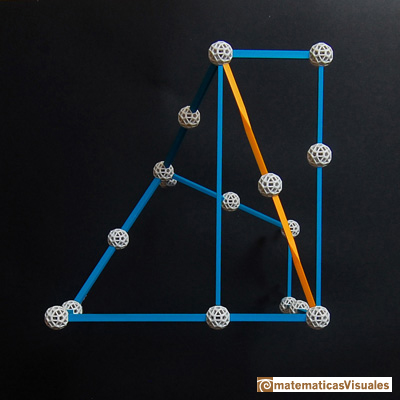
The volume of a tetrahedron is one third of the prism that contains it.

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.

The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.

The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.

You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.

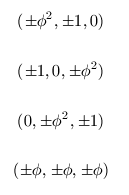
 is the golden ratio we've seen in the golden rectangle.
is the golden ratio we've seen in the golden rectangle.



















 PREVIOUS
PREVIOUS































 NEXT
NEXT







