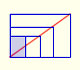
Truncating a polyhedron means that the corners (or the edges) are cut off.
We have already study several cases of truncating the vertices of regular polyhedra.
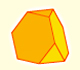
The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.
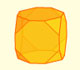
When you truncate a cube you get a truncated cube and a cuboctahedron. If you truncate an octahedron you get a truncated octahedron and a cuboctahedron.
In this page we are going to see the truncation of the edges of a cube and we are going to get a new polyhedron called the chamfered cube.
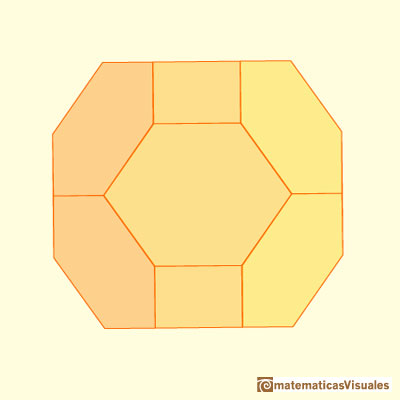
You can get a polyhedron with all the edges of equal length. Then the twelve hexagons are equilateral but no equiangular.
The chamfered cube is a polyhedron that is similar to the truncated octahedron. But the truncated octahedron have twelve hexagons that are regular.

The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
Hexagons in a truncated octahedron are equilateral and equiangular.
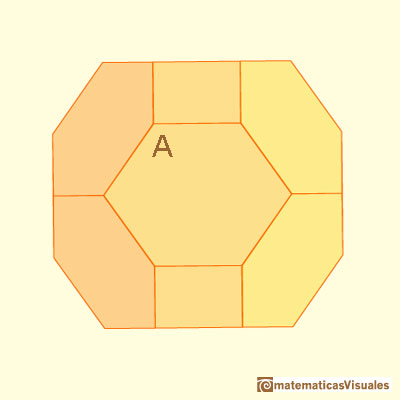
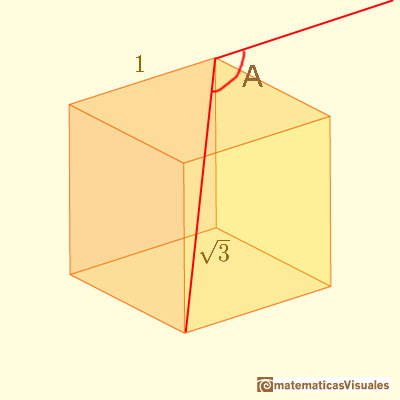
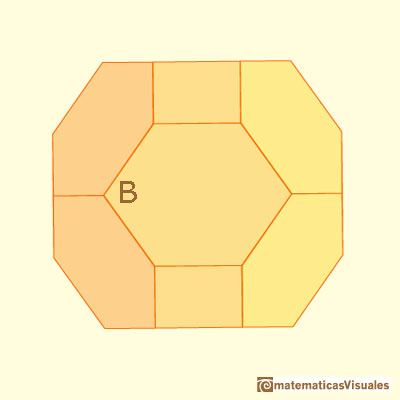
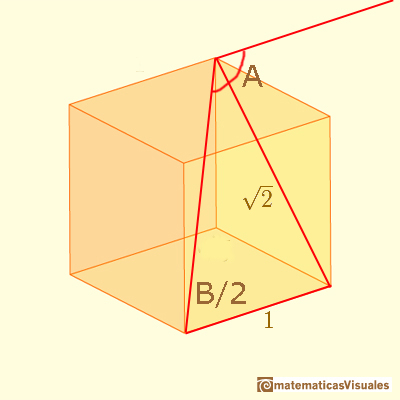
To see that the hexagons in a chamfered cube are not equiangular we are going to calculate these angles.
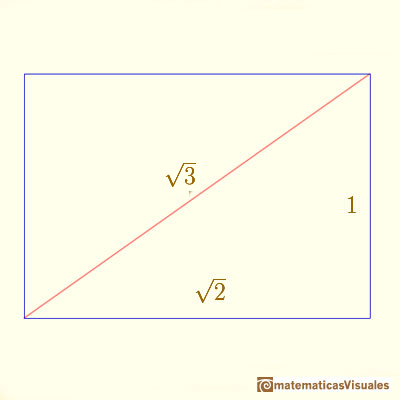
Angles of this polyhedron are related with angles we found studying the DinA4 rectangle.
You can calculate angle A:
Then angle B:
In fact
As a limiting case you get a polyhedron with very interesting properties: the rhombic dodecahedron.
The rhombic dodecahedron and the cuboctahedron are dual polyhedra.
The chamfered cube with all edges of equal length is also called truncated rhombic dodecahedron because you can get this polyhedron by truncating
the six vertices of orden 4 of a rhombic dodecahedron is such a way that the truncated vertices become squares and the rhombic faces become equilateral but not regular hexagons.
MORE LINKS

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.

The volume of a tetrahedron is one third of the prism that contains it.

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.

We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.

Plane developments of cones and conical frustum. How to calculate the lateral surface area.
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
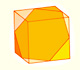
We can cut in half a cube by a plane and get a section that is a regular hexagon. Using eight of this pieces we can made a truncated octahedron.

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron

The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.

These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.

The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.

The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.

The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.

A very simple technique to build complex and colorful polyhedra.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).








 NEXT
NEXT
 PREVIOUS
PREVIOUS