A right prism is a polyhedron that has two congruents pararel polygonal faces (bases of the prism) and with all remaining faces are rectangles.
The main interest of this page is to see how a right prism can be developed into a plane net.
There is a platonic solid that is a prism, the cube. This is a cube net:
The lateral surface area of a prism is the sum of the areas of the rectangles that form the faces that are not bases of the prism.
We can calculate the lateral surface area of a right prism (p is the perimeter of a base and h is the height of the prism):
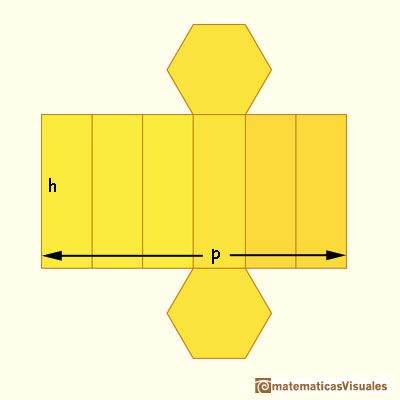
In the examples above bases were regular polygons. But we can consider prisms whose bases are not regular polygons. In the next mathlet,
bases are non-regular polygons (although they are inscribed in a circle and they are convex polygons). Each time we change the number of sides of the base a new prism is generated
with sides randomly drawn:
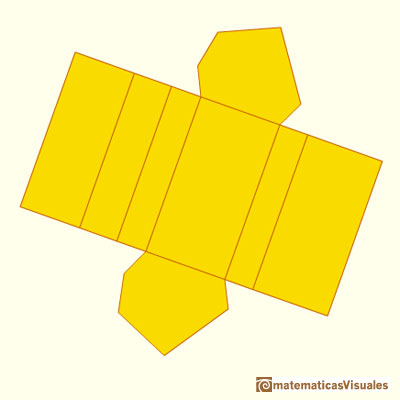
A non-regular hexagonal prism:
And its plane net:
Another example, plane net of a non-regular triangular prism:
The formula for calculating the lateral surface area is the same as before.
MORE LINKS
We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.
We study different cylinders cut by an oblique plane. The section that we get is an ellipse.
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.
Plane net of pyramids cut by an oblique plane.
Plane developments of cones and conical frustum. How to calculate the lateral surface area.
Plane developments of cones cut by an oblique plane. The section is an ellipse.
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
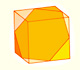
We can cut in half a cube by a plane and get a section that is a regular hexagon. Using eight of this pieces we can made a truncated octahedron.
Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
The volume of a tetrahedron is one third of the prism that contains it.
The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.
A very simple technique to build complex and colorful polyhedra.
NEXT
