Hilbert and Cohn-Vossen wrote about the cylinder: "The circular cylinder is the simplest curved surface. It can be obtained from the
simplest curves -the straight line and the circle- by moving a straight line around the circunference of a circle while keeping it
perpendicular to the plane of the circle. Another way to get the cylinder is by rotating a straight line about an axis parallel to
it. Thus the circular cylinder is a surface of revolution. The surfaces of revolution are an important class of surfaces, characterized
by the property that they can be generated by rotating a plane curve about an axis lying in the plane of the curve."
(Hilber and Cohn-Vossen. Geometry and the Imagination. pag. 7).
In this page, the cylinder will be closed by two parallel planes perpendicular to the axis. These planes intersect the cylinder in two
circles. We call these circles the bases of the cylinder.
The main interest of this page is to see how a cylinder can be developed into a plane.
The lateral surface area of a cylinder is the area of a rectangle. The length of this rectangle is the circunference
of one of the bases of the cylinder.
We can calculate the lateral surface area of a cylinder:
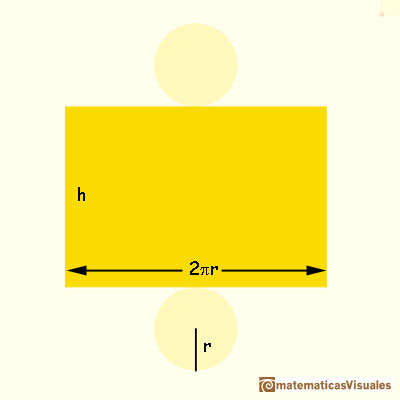
To calculate the Total Surface Area of a cylinder we must add the lateral surface area plus the top and bottom circles (the two circles that
make up the ends of the cylinder). Then:
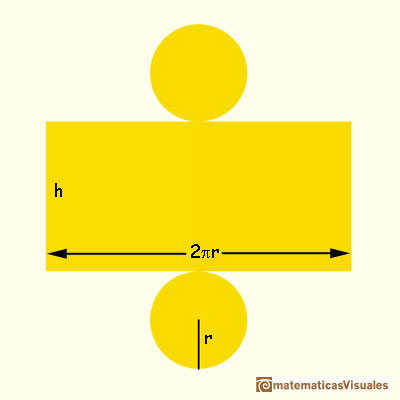
Do you remember how to calculate the volume of a cylinder?
MORE LINKS
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.
Plane net of pyramids cut by an oblique plane.
Plane developments of cones and conical frustum. How to calculate the lateral surface area.
Plane developments of cones cut by an oblique plane. The section is an ellipse.
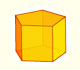
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.
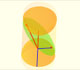
The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.
Durer was the first who published in german a method to draw ellipses as cone sections.
Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .
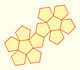
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
Using Cavalieri's Principle we can calculate the volume of a sphere.
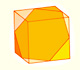
We can cut in half a cube by a plane and get a section that is a regular hexagon. Using eight of this pieces we can made a truncated octahedron.
Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
The volume of a tetrahedron is one third of the prism that contains it.
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.
A very simple technique to build complex and colorful polyhedra.
NEXT
PREVIOUS
