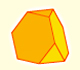
|
|
|
Truncated Octahedron (adapted from Leonardo da Vinci)
This video is an adaptation of the drawing that Leonardo da Vinci made of the truncated octahedron (octocedron abscisus vacuus) for Luca Pacioli's book 'De Divina Proportione'.
Pacioli wrote about the truncated octahedron (Spanish translation):
"El octaedro abciso o cortado plano sólido o hueco tiene treinta y seis líneas que forman setenta y dos ángulos superficiales,
cuarenta y ocho de los cuales pertenecen a los hexágonos y veinticuatro a los cuadrados, y contiene veinticuatro ángulos sólidos y
catorce bases, ocho de las cuales son hexagonales, o sea, de seis lados, y seis tetragonales, o sea cuadradas. Pero veinticuatro
de las mencionadas líneas son comunes a los cuadrados y a los hexágonos. Los cuadrados están formados a partir de los hexágonos que,
en número de ocho, se tocan de modo uniforme, como nos hace ver claramente el intelecto en su forma material."
('La divina proporción' de Luca Pacioli, page 93, Spanish translation by Juan Calatrava, Editorial Akal, 4th edition, 2008)
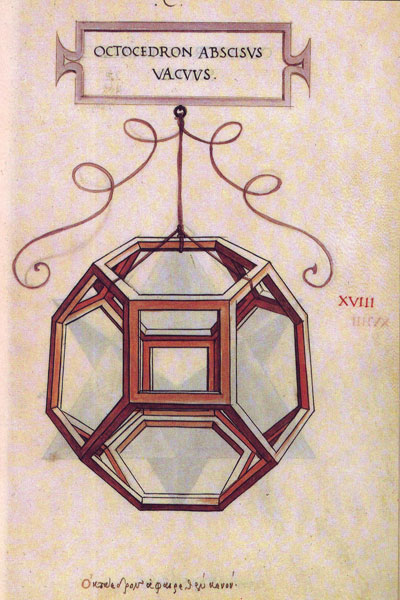
Leonardo da Vinci's drawing of the truncated octahedron (octocedron abscisus vacuus) for Luca Pacioli's book 'De divina proportione'. (There is an Spanish version, 'La divina proporción' Editorial Akal. Image used with permission of Editorial Akal).
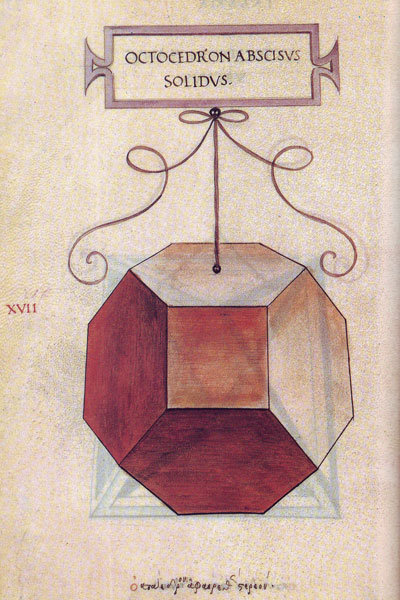
Leonardo da Vinci's drawing of the truncated octahedron (octocedron abscisus solidus) for Luca Pacioli's book 'De divina proportione'. (There is an Spanish version, 'La divina proporción' Editorial Akal. Image used with permission of Editorial Akal).
If you play with the interactive application you can get images like these:
REFERENCES
Luca Pacioli - La divina proporción - Ediciones Akal, 4th edition, 2004. Spanish edition of 'De divina proportione'. Translation by Juan Calatrava.
Leonardo da Vinci's Geometric Sketches Frank J. Swetz's article in MathDl, Loci:Convergence.
Leonardo da Vinci's Polyhedra George Hart's excellent website about polyhedra.
NEXT
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.
PREVIOUS
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.
MORE LINKS
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated tetrahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the octahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the rhombicuboctahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the Campanus' sphere.
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.
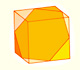
We can cut in half a cube by a plane and get a section that is a regular hexagon. Using eight of this pieces we can made a truncated octahedron.
Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.
One eighth of a regular dodecahedon of edge 2 has the same volume as a dodecahedron of edge 1.
The volume of a tetrahedron is one third of the prism that contains it.
The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.
The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.
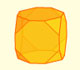
When you truncate a cube you get a truncated cube and a cuboctahedron. If you truncate an octahedron you get a truncated octahedron and a cuboctahedron.
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.