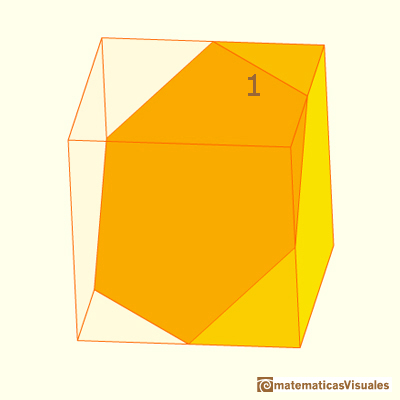
A cube intersected by a plane perpendicular to its diagonal can be cut in half. We get a section that is a regular hexagon.
You can see this model of the hexagonal section of a cube in the Deutsches Museum, the Science Museum in Munich:
This polyhedron has very interesting properties. In this page we are going to study two of these properties: its volume
is very easy to calculate and this body fills the space (tessellation).
To calculate the volume we can start calculating the volume of a cube given the length of the diagonal of one face.
For example, if the diagonal length is equal to 2, then the volume:
Then, the volume of half a cube:
The second property is that this body is a space-filling polyhedron: it is a polyhedron that generates a tessellation of space.
This is clear because the cube is the simplest space-filling polyhedron and our body is only half a cube.
This property is going to have interesting consequences.
Using eight of these half cubes we can build a truncated octahedron.
This relation between the cube and the truncated octahedron can help us to understand that the
truncated octahedron is a space-filling polyhedron.
MORE LINKS

These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.
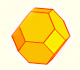
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.

The volume of a tetrahedron is one third of the prism that contains it.

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.

The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.

Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.
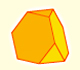
The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.
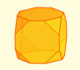
When you truncate a cube you get a truncated cube and a cuboctahedron. If you truncate an octahedron you get a truncated octahedron and a cuboctahedron.
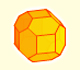
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.











 NEXT
NEXT



























