Truncating a polyhedron means that the corners (or the edges) are cut off.
Starting with Platonic solids (regular polyhedra) and symmetrically slicing away the corners we get some Archimedean solids (semi-regular polyhedra).
We have already study the truncated tetrahedron that is the single archimedean polyhedron that is obtained by truncating the tetrahedron.
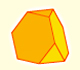
The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.
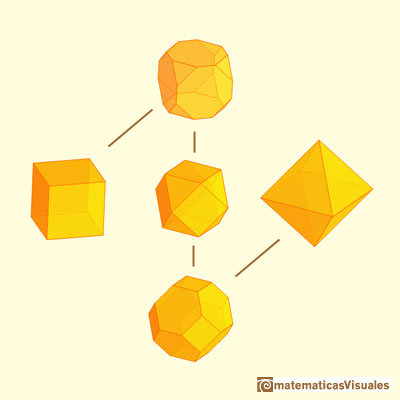
We are going to investigate truncations of a cube and an octahedron. They are related because cube and octahedron are dual polyhedra.
Starting with a cube you can remove the corners to make equilateral triangles.
If we remove the eight corners in such a way that the original square faces of the cube become regular octagons the results is the truncated cube.
The truncated cube (or truncated hexahedron) is an archimedean solid. It has 14 regular faces (6 octogons and 8 triangles).
You can make a truncated cube very easily with cardboard and rubber bands:
Truncated cube lamp in the Palau Baro of Quadras, a modernist building in Barcelona (Spain)
If our truncation is deeper we get another archimedean solid, the cuboctahedron. It has six squares and eight triangles.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.
You can also get a cuboctahedron truncating an octahedron.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.
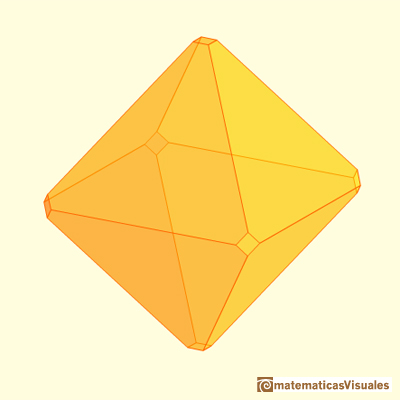
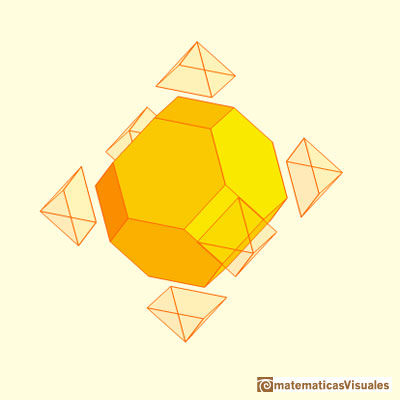
Another truncation of the octahedron is called the truncated octahedron with six square faces and eight hexagonal faces.
Since four faces meet at the vertexes of the octahedron, cutting off its corners makes squares, and the original triangular faces become hexagons.
It is another archimedean solid.

The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.

These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
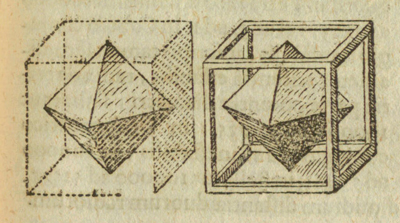
The cuboctahedron is related with the duality between the cube and the octahedron:
Kepler was aware of this relation:
The first stellation of the cuboctahedron is the compound of a cube and its dual octahedron, with the vertices of the cuboctahedron
located at the midpoints of the edges. It is the same to say that the solid common to both the cube and the octahedron in a
cube-octahedron compound is a cuboctahedron.

The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.
The vertices of a stellated cuboctahedron are the vertices of a rhombic dodecahedron (that is the dual polyhedra of a cuboctahedron).
REFERENCES
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
MORE LINKS

You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.

These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.

A very simple technique to build complex and colorful polyhedra.

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.

We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.

Plane developments of cones and conical frustum. How to calculate the lateral surface area.
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .




















 NEXT
NEXT

























 PREVIOUS
PREVIOUS



