Bonaventura Cavalieri(1598-1647) was an italian mathematician. He was a precursor of infinitesimal calculus. Cavalieri, Kepler and other mathematicians, who lived during the century preceding Newton and Leibniz, invented and used intuitive infinitesimal methods to solve area and volume problems.

Twenty years after the publication of Kepler's Stereometria Doliorum, Cavalieri wrote a very popular book: Geometria indivisibilibus (1635).

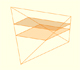
In this book, the Italian mathematician used what is now known as Cavalieri's Principle: If two solids have equal altitudes, and if sections made by planes parallel to the bases and at equal distances from them are always in a given ratio, then the volumes of the solids are also in this ratio.

Cavalieri's Principle is also call the method of indivisibles. "Cavalieri made the notion of the indivisible the basis of a geometrical method of demonstration. He didn't explained precisely what he understood by the word indivisible, which he employed to characterize the infinitesimal elements used in his method. Cavalieri conceived of a surface as made up an indefinite number of equidistant parallel lines and of a solid as composed of parallel equidistant planes, these elements being designated the indivisibles of the surface and of the volume respectively." (C.H. Edwards)

Zu Geng, born about 450, was a chinese mathematician who used what is now know as the Principle of Liu Hui and Zu Geng to calculate the volume of a sphere. Liu-Zu theory is equivalent to Cavalieri's Principle. Then, chinese mathematicians had used this principle for more than one millennium before Cavalieri. You can read a biography of Zu Geng in MacTutor and the article Zu-Geng's axiom vs Cavalieri's theory by Ji-Huan He.

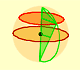
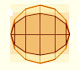
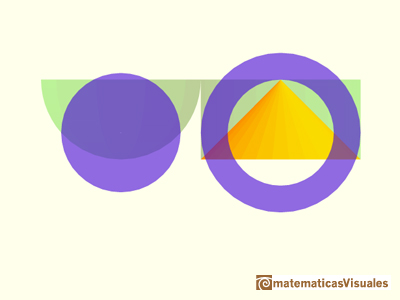
A well known application of Cavalieri's Principle is used to calculate the volume of a sphere. We can compare the area of a section of an hemisphere and the area of a section of a body that is a cylinder minus a cone.

This two areas are equal. Then the two bodies have the same volume. It is very easy to calculate the volume of the second body(because we know how to calculate the volume of a cylinder minus the volume of a cone), then we get the volume of the hemisphere.

We need to probe that the area of the disc is equal to the area of the annulus (for each section):

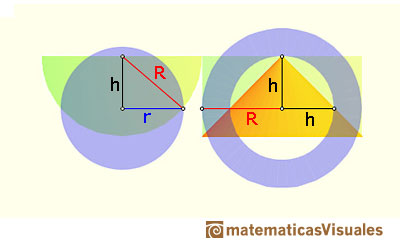
For each altitude h, the area of the disc is:

and the area of the annulus is:

Then, for each altitude the two sections have equal area.

Using Cavalieri's Principle we can deduce:

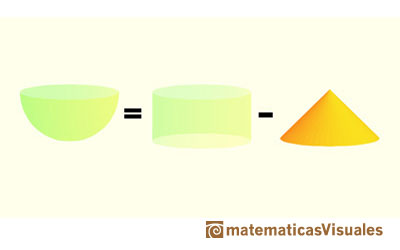
Using the formulas for the volume of a cylinder and of a cone we can write the volume of an hemisphere:

Then, the volume of a sphere of radius R is (as Archimedes already knew, 1800 years before):

MORE LINKS

Pythagoras Theorem: Euclid's demonstration

Demonstration of Pythagoras Theorem inspired in Euclid.

Kepler: The Area of a Circle

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.

Kepler: The best proportions for a wine barrel

Studying the volume of a barrel, Kepler solved a problem about maxima in 1615.

Campanus' sphere and other polyhedra inscribed in a sphere

We study a kind of polyhedra inscribed in a sphere, in particular the Campanus' sphere that was very popular during the Renaissance.

Leonardo da Vinci:Drawing of a SEPTUAGINTA made to Luca Pacioli's De divina proportione.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the Campanus' sphere.

Sections in Howard Eves's tetrahedron

In his article 'Two Surprising Theorems on Cavalieri Congruence' Howard Eves describes an interesting tetrahedron. In this page we calculate its cross-section areas and its volume.

Surprising Cavalieri congruence between a sphere and a tetrahedron

Howard Eves's tetrahedron is Cavalieri congruent with a given sphere. You can see that corresponding sections have the same area. Then the volumen of the sphere is the same as the volume of the tetrahedron. And we know how to calculate this volumen.

Sections on a tetrahedron

Special sections of a tetrahedron are rectangles (and even squares). We can calculate the area of these cross-sections.

Archimedes' Method to calculate the area of a parabolic segment

Archimedes show us in 'The Method' how to use the lever law to discover the area of a parabolic segment.

Archimedes and the area of an ellipse: an intuitive approach

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.

Archimedes and the area of an ellipse: Demonstration

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.