Howard Eves received the George Polya Award for the article Two Surprising Theorems on Cavalieri Congruence.
In this article he wrote a brief biography of Cavalieri (1598-1647): "Cavalieri was one of the most influential mathematicians of his time, and the author of a number of works on trigonometry, geometry, optics, astronomy and astrology. He was among the first to recognize the great value of logarithms and was largely responsible for their introduction into Italy. But his greatest contribution to mathematics was a treatise, Geometria indivisibilibus, published in its first form in 1635, devoted to the precalculus method of indivisibles."
"Cavalieri's treatise on the method of indivisibles is voluable and not clearly written, and it is not easy to learn from it precisely what Cavalieri meant by an 'indivisible'. It seems that an indivisible of a given planar piece is a chord of the piece, and a planar piece can be considered as made up of an infinite parallel set of such indivisibles. Similarly, it seems that an indivisible of a given solid is a planar section of that solid, and a solid can be considered as made up of an infinite parallel set of this kind of indivisibles. Now, Cavalieri argued, if we slide each member of a parallel set of indivisibles of some planar piece along its own axis, so that the endpoints of the indivisibles still trace a continuous boundary, then the area of the new planar piece so formed is the same as that of the original planar piece, inasmuch as the two pieces are made up of the same indivisibles. A similar sliding of the members of a parallel set of indivisibles of a given solid will yield another solid having the same volume as the original one." (H. Eves)
"Accepting Cavalieri's principles as intuitively evident, one can solve many problems in mensuration that normally require the more advanced techniques of the calculus. Let us define two planar pieces that can be placed so that they cut off equal segments on each member of a family of parallel lines, or two solids that can be placed so that they intersect equiareal sections on each members of a family of parallel planes, to be Cavalieri congruent. To find the unknown area of some planar piece, or the unknown volume of some solid, one tries to find a comparaison figure of easily found area or volumen that is Cavalieri congruent to the given figure." (H. Eves)
One of the purposes of Eves' article is to prove something that is difficult to believe, that there exists a polyhedron to which a given sphere is Cavalieri congruent. "A sphere is so round, and a polyhedron is so angular and made up of nothing but planes! Nevertheless, we will prove that there exists a polyhedron (actually a tetrahedron) to which a given sphere is Cavalieri congruent." (H. Eves)
We have seen that the areas of the sections in one sphere are:
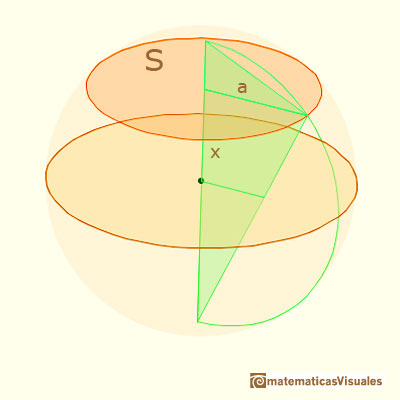
The corresponding areas of the sections in the Howard Eves's tetrahedron are equal
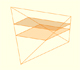
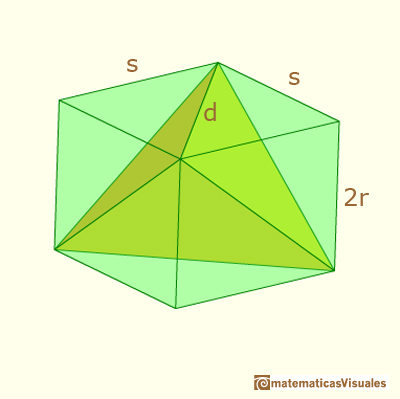
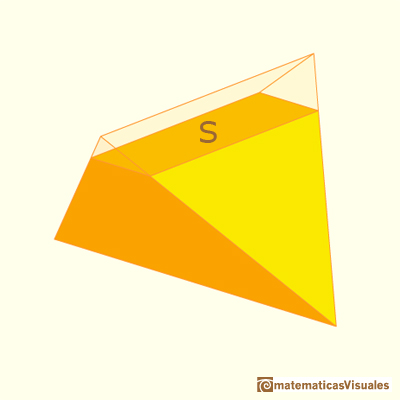
The volume of Howard Eves' tetrahedron is:

Therefore, Howard Eves claims that
"Theorem 2. There exist a tetrahedron to witch a give sphere is Cavalieri congruent."
Then, the volume of the sphere is the same as the volume of the tetrahedron:
REFERENCES
 PREVIOUS
PREVIOUS
MORE LINKS




















 NEXT
NEXT