After studying Campanus' sphere and other polyhedra inscribed in a sphere it seems natural to me to develop a simple map of the World.

Campanus' sphere and other polyhedra inscribed in a sphere

We study a kind of polyhedra inscribed in a sphere, in particular the Campanus' sphere that was very popular during the Renaissance.

Roughly speaking the Earth rotates around an imaginary axis that passes through two points on the Earth's surface called North Pole and South Pole.

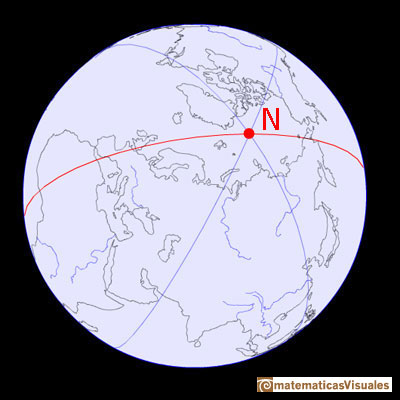
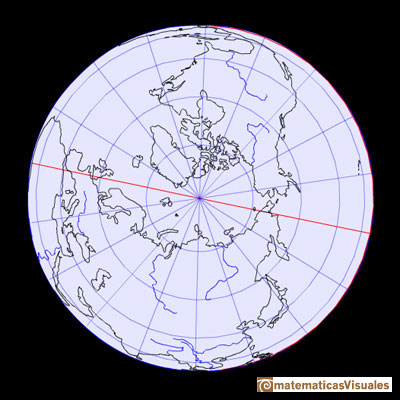
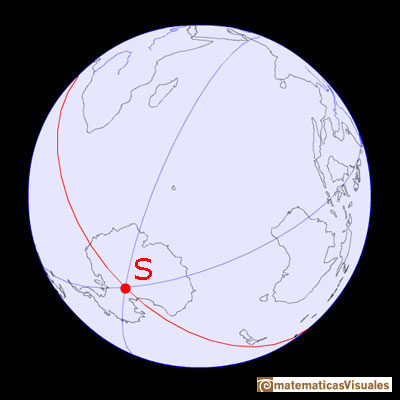
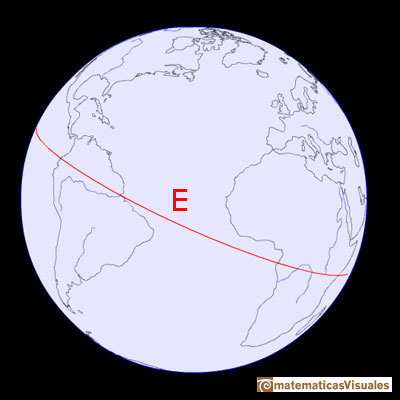
The Equator is the intersection between the Earth and a plane perpendicular at the midpoint of it axis.

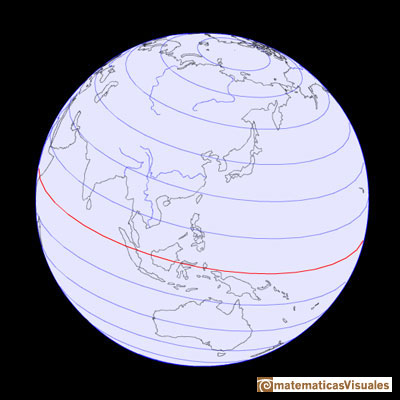
The circles of latitud are parallels to the equator. They are called parallels because of that. The circles of latitude get smaller as the distance from the Equator increases

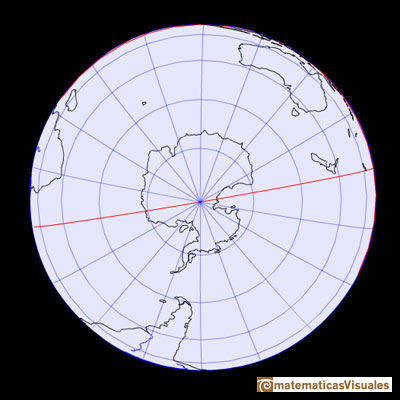
Latitude is a measurement of the distance north or south of the Equator. It is measured in degrees. The equator is defined as 0 degrees, the North Pole is 90 degrees north, and the South Pole is 90 degrees south.

Circles of longitud are great circles that passes through the two poles. They are known as meridians. One important (and arbitrary) meridian runs through the Royal Observatory in Greenwich, England. We call it the Prime Meridian.

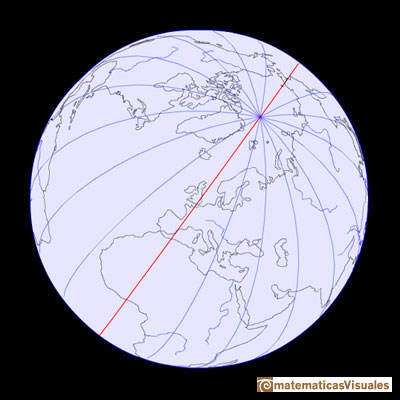
Longitude is measured in degrees east or west of the prime meridian The prime meridian is assigned the value of 0 degrees.

Latitude and longitude lines are a grid map. A geografic coordinate system so we can now locate every point on Earth by specifying both latitude and longitude.

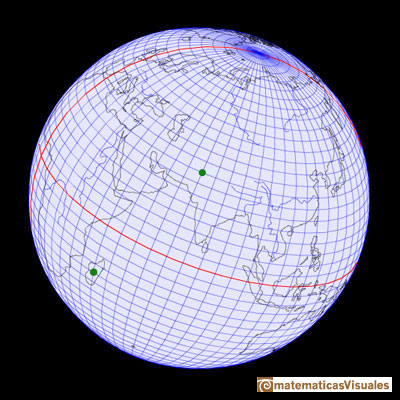
Playing with the interactive application you can rotate the Earth and control the number of parallels and meridians you want to see.

MORE LINKS

Leonardo da Vinci:Drawing of a SEPTUAGINTA made to Luca Pacioli's De divina proportione.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the Campanus' sphere.

Cavalieri: The volume of a sphere

Using Cavalieri's Principle we can calculate the volume of a sphere.

Kepler: The Area of a Circle

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.

Sections in Howard Eves's tetrahedron

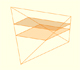
In his article 'Two Surprising Theorems on Cavalieri Congruence' Howard Eves describes an interesting tetrahedron. In this page we calculate its cross-section areas and its volume.

Surprising Cavalieri congruence between a sphere and a tetrahedron

Howard Eves's tetrahedron is Cavalieri congruent with a given sphere. You can see that corresponding sections have the same area. Then the volumen of the sphere is the same as the volume of the tetrahedron. And we know how to calculate this volumen.

Sections on a tetrahedron

Special sections of a tetrahedron are rectangles (and even squares). We can calculate the area of these cross-sections.