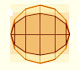
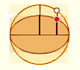
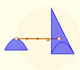
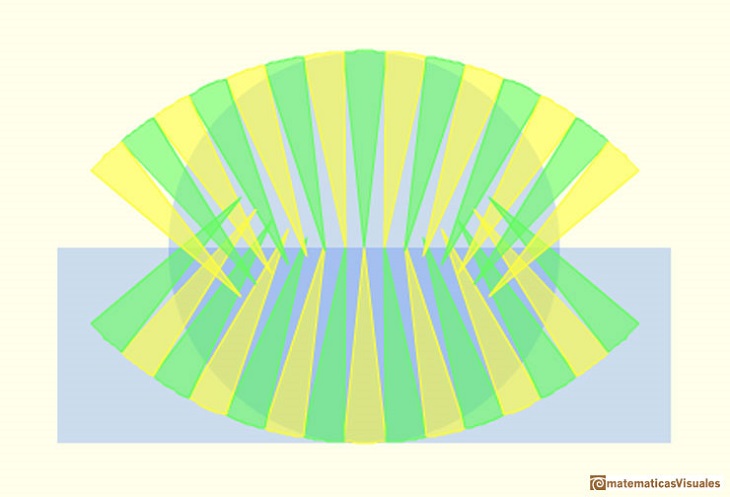
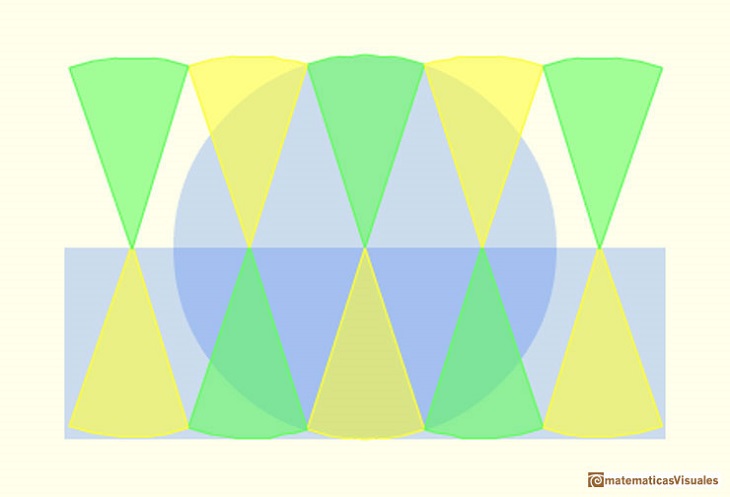
Kepler wrote Nova stereometria doliorum vinariorum (New solid geometry of wine barrel) in 1615. This book is a systematic work on the calculation of areas and volumes by infinitesimal techniques. Kepler opens his book with the problem of determining the area of the circle. He regarded the circle as a regular polygon with an infinite number of sides, and its area is made up of infinitesimal triangles. (See Boyer, p. 108)



The perimeter of a circle is called the circunference. If r is the radius of the circle and d is the diameter we can write the circunference as:
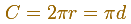
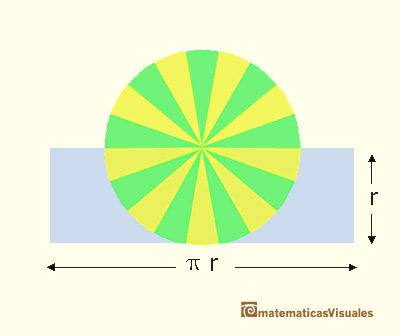
then we can deduce the area of the circle:
Margaret Baron wrote about this aspect of Kepler's work: "Of the circle he says that the circunference has as many parts as it has points, each part forming the base of an isosceles triangle with vertex at the center of the circle. The circle is accordingly made up of an infinity of small triangles, each with its base on the circunference and with altitude equal to the radius of the circle. Replacing these triangles by a single triangle with the circunference as base the area of the circle is thus given in terms of the circunference and radius." (Baron, p. 110).
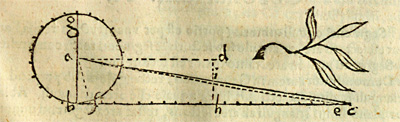
This is the original drawing in Kepler's book. We can read this page, and the full book, in The Posner Memorial Collection,Carnegie Mellon University Libraries
REFERENCES
 NEXT
NEXT
MORE LINKS