Archimedes was born in Syracuse (a Greek city in what is now Sicily) around 287 BC and he was killed in 212 BC when Syracuse fell to the Romans.

"Among his most famous results were the volume and surface area of the sphere and the area of a parabolic segment. Archimedes first discovered these results by nonrigorous methods, later confirming them by the method of exhaustion." (Stillwell)

In his work "The Method", Archimedes wrote about his method of discovery. Archimedes "mechanical method" is based on the law of the lever. "In it Archimedes disclosed the method which is presumably that which he employed in reaching many of his conclusions in problems involving areas and volumes. Realizing that it is avantageous to have a preliminary notion of the result before carrying through a deductive geometrical demonstration, Archimedes employed for this purpose, in conjunction with his law of the lever, the idea of a surface as made up of lines." (Boyer)

Here we try to show how Archimedes discovered the area of a segment of a parabola.

The area of a parabolic segment is 4/3 the triangle having the same base and vertex.

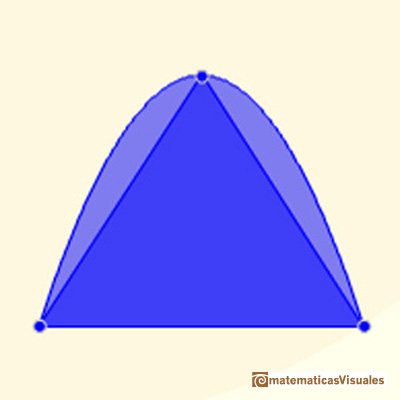
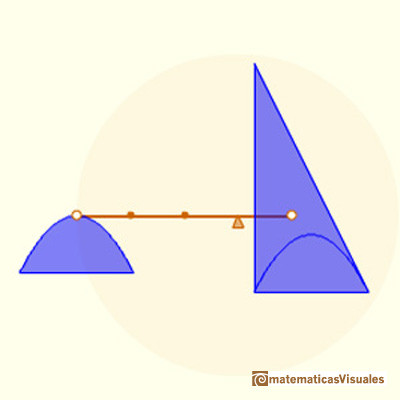
He considered a second triangle using a tangent. This triangle is 4 time the first. And the are of this second triangle is 1/3 the area of the parabolic segment.

The parabolic segment and the second triangle will be in equilibrium:

The construction from Archimedes is more general than ours. Here is the explanation we can read in Boyer's book:

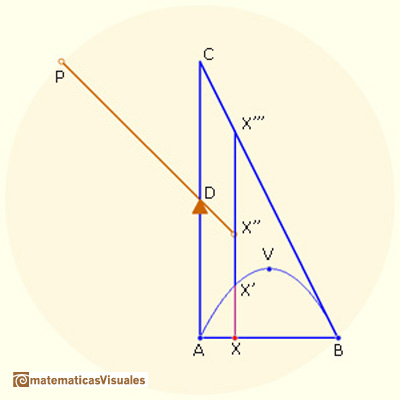
"V is the vertex of the parabola, BC is tangent at B, BD = DP, and X is any point on AB, we know from the properties of the parabola that for any position of X we have the ratio

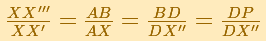
But X'' is the center of gravity of XX''', so that from the law of the lever we see that XX', if brought to P as its midpoint, will balance XX''' in its present position. This will be true for all position of X on AB. Inasmuch as the triangle ABC consists of the straight lines XX''' in this triangle, and since the parabolic segment AVB is likewise made up of the lines XX', we can conclude that the triangle ABC in its present position will be in equilibrium at D with the parabolic segment when this is transferred to P as its center of gravity. But the center of gravity of ABC is on BD and is 1/3 the distance from D to B, so that the segment AVB is 1/3 the triangle ABC, or 4/3 the triangle AVB."(Boyer)

LINKS

Archimedes and the area of an ellipse: an intuitive approach

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.

Archimedes and the area of an ellipse: Demonstration

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.

Kepler: The Area of a Circle

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.

Kepler: Surface and volume of a sphere

Kepler studied the volume and surface of the sphere. He thought the volume of the sphere as made up of small cones, then he sum all of these cones and get a relation between the surface of a sphere en its volume.

Kepler: The volume of a wine barrel

Kepler was one mathematician who contributed to the origin of integral calculus. He used infinitesimal techniques for calculating areas and volumes.

Kepler: The best proportions for a wine barrel

Studying the volume of a barrel, Kepler solved a problem about maxima in 1615.

Cavalieri: The volume of a sphere

Using Cavalieri's Principle we can calculate the volume of a sphere.

Surprising Cavalieri congruence between a sphere and a tetrahedron

Howard Eves's tetrahedron is Cavalieri congruent with a given sphere. You can see that corresponding sections have the same area. Then the volumen of the sphere is the same as the volume of the tetrahedron. And we know how to calculate this volumen.

Integral of powers with natural exponent

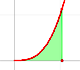
The integral of power functions was know by Cavalieri from n=1 to n=9. Fermat was able to solve this problem using geometric progressions.

Pythagoras' Theorem in a tiling

We can see Pythagoras' Theorem in a tiling. It is a graphic demonstration of Pythagoras' Theorem we can see in some floor made using squares of two different sizes.