Very little is known for certain about Pythagoras. Probably he was born on Samos around 580 BC. He founded a school in Croton, a Greek colony in what is now southern Italy.
You can play with a demonstration of the Pythagoras' theorem inspired in Euclid in the next link:

Demonstration of Pythagoras Theorem inspired in Euclid.
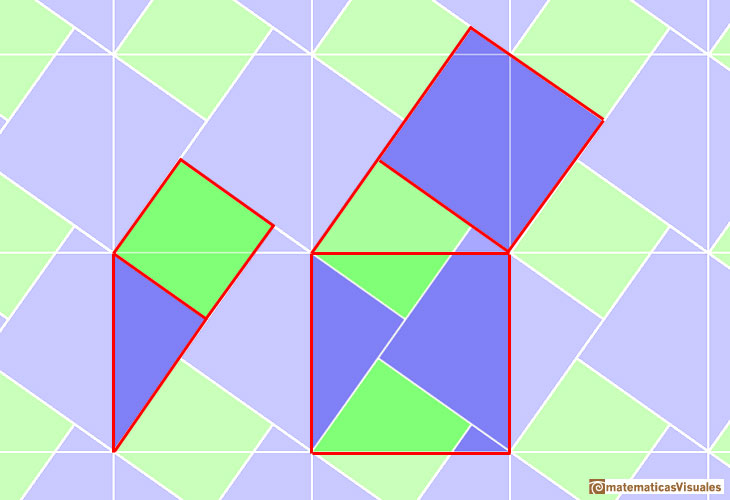
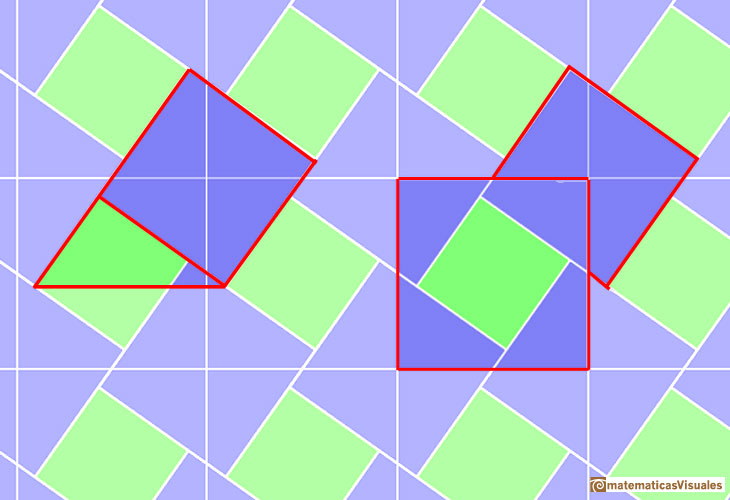
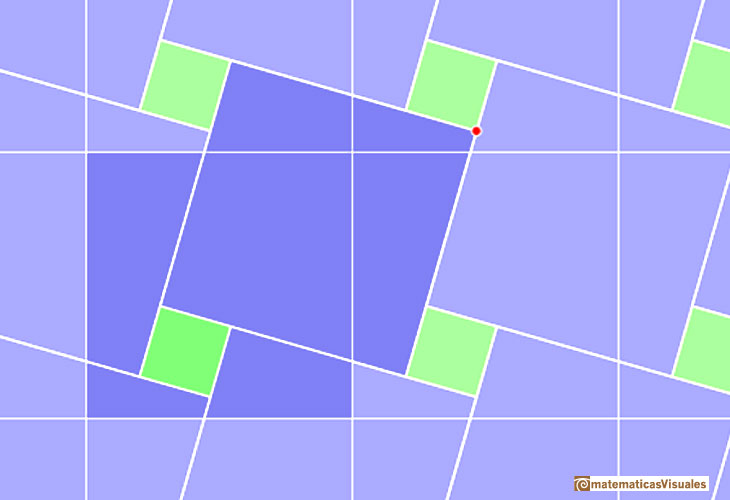
Here we show Pythagoras' theorem in a tiling. This tiling can be seen in floors, for example.
This tiling is made using two kind of squares (green and blue). These are the squares of the two legs of a right triangle.
We can draw a chessboard tesselation which is made of squares that are the squares of the hypotenuse.
Then we can see the right triangle:
"It is intuitively clear that the two
tiles (big square and union of two smaller squares) must have the same area.
Indeed, this statement is simply the Pythagorean theorem, and it has been
conjectured that it was discovered by a contemplation of tiling designs.
(...). From an axiomatic point of view, this proof is a
particularly economical one since it shows that the two smaller squares can
be dissected into a bounded number of pieces which then can be put together
in such a manner that they just fill the big square." (Magnus, p. 53)
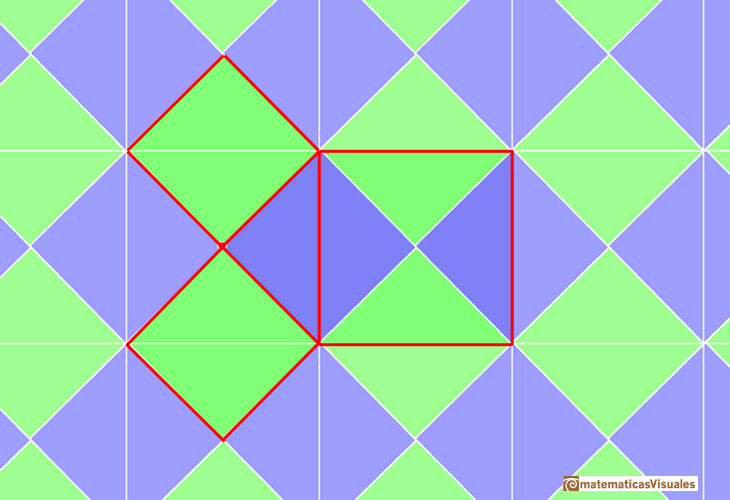
The simplest case is about an isosceles right triangle. Then the squares on the two legs are equal. These two squares are made of four congruent triangles (half a square)
that fit together to form the square on the hypotenuse.
REFERENCES
John Stillwell, "Mathematics and its History", Springer-Verlag, New York, 2002.
Euclides, The Elements
W. Magnus, "Noneuclidean Tesselations and Their Groups", Academic Press, New York-London, 1973.
H.S.M. Coxeter, 'Introduction to Geometry', John Wiley and Sons, Second edition, pp. 8-9.
Martin Gardner, 'Sixth Book of Mathematical Diversions from "Scientific American"'. Scribner, 1975.
Eli Maor, "The Pythagorean theorem: a 4000-year history", Princeton University Press, United States of America, 2007.
Greg N. Frederikson, "Dissections, Plane and Fancy", Cambridge University Press, United States of America, 1997.
F.J. Swetz and T.I. Kao, "Was Pythagoras chinese?", The Pennsylvania State University Press, United States of America, 1977.
MORE LINKS
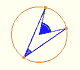
Central angle in a circle is twice the angle inscribed in the circle.
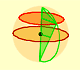
We want to calculate the surface area of sections of a sphere using the Pythagorean Theorem. We also study the relation with the Geometric Mean and the Right Triangle Altitude Theorem.
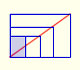
There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.
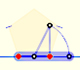
You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.

Using Cavalieri's Principle we can calculate the volume of a sphere.

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron

The volume of a tetrahedron is one third of the prism that contains it.

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
In his article 'Two Surprising Theorems on Cavalieri Congruence' Howard Eves describes an interesting tetrahedron. In this page we calculate its cross-section areas and its volume.

Howard Eves's tetrahedron is Cavalieri congruent with a given sphere. You can see that corresponding sections have the same area. Then the volumen of the sphere is the same as the volume of the tetrahedron. And we know how to calculate this volumen.

Studying the volume of a barrel, Kepler solved a problem about maxima in 1615.



 PREVIOUS
PREVIOUS





















 NEXT
NEXT




