|
|
|
Archimedes got an ellipse shrinking a circle along one direction. Then Archimedes could deduce the area of an ellipse as a generalization of the area of a circle.
From the implicit equation of a circle
we can deduce one equation of an ellipse.
When we shrink the circle, each point on the circle goes to a point on the ellipse. Then if a point P with coordinates (x,y) is on the ellipse E then its corresponding point is on the circle C.
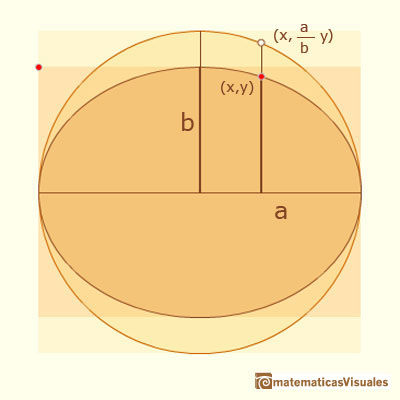
Using the implicit equation of a circle and the coordinates of these corresponding points on the circle we can write:
Dividing by a square we get the implicit equation of an ellipse:
A circle is a special case of an ellipse (when a = b).
NEXT
Every ellipse has two foci and if we add the distance between a point on the ellipse and these two foci we get a constant.
MORE LINKS
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.
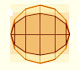
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.
An Ellipsograph is a mechanical device used for drawing ellipses.
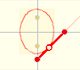
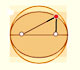
If a straight-line segment is moved in such a way that its extremities travel on two mutually perpendicular straight lines then the midpoint traces out a circle; every other point of the line traces out an ellipse.
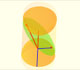
The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.
Durer was the first who published in german a method to draw ellipses as cone sections.
Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .
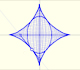
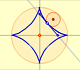
The Astroid is the envelope of a segment of constant length moving with its ends upon two perpendicular lines. It is also the envelope of a family of ellipses, the sum of whose axes is constant.
The Astroid is a particular case of a family of curves called hypocycloids.
We study different cylinders cut by an oblique plane. The section that we get is an ellipse.
Plane developments of cones cut by an oblique plane. The section is an ellipse.
Kepler used an intuitive infinitesimal approach to calculate the area of a circle.
The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.