We have already studied the Ellipsograph or "Trammel of Archimedes". It is a device that consists of a rod that is moving with two fixed points
upon two fixed perpendicular lines.

An Ellipsograph is a mechanical device used for drawing ellipses.
We know that every point on this rod draws an ellipse.
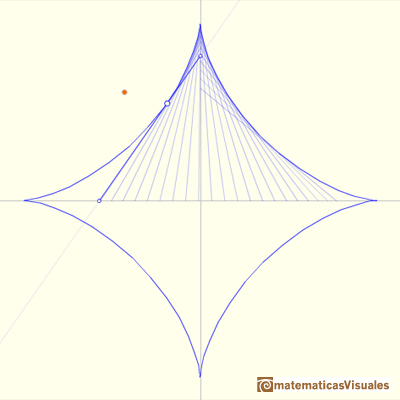
We turn our attention to the moving segment of constant length. We can see this segment as an sliding ladder.
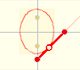
If a straight-line segment is moved in such a way that its extremities travel on two mutually perpendicular straight lines then the midpoint traces out a circle; every other point of the line traces out an ellipse.
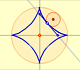
If we consider the envelope of this lines of constant length moving with its ends upon two perpendicular lines the result is a curve
that has four cups. Its name is Astroid.
You can play with the first interactive application to see the moving segment and the astroid.
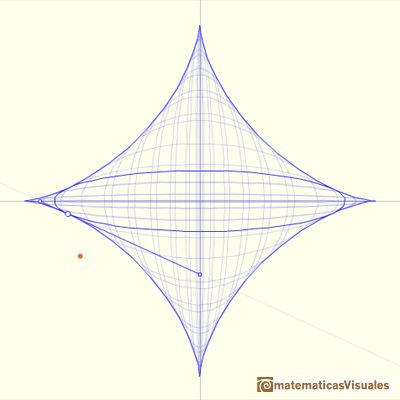
The Astroid is also the envelopè of a family of ellipses, the sum of whose axes is constant (the length of the moving segment).
Playing with the next interactive application you can see the astroid and the family of ellipses.
REFERENCES
Tom Apostol and Mamikon Mnatsakanian, 'New Horizons in Geometry' (Chapter 9. Trammels, ), Mathematical Association of America, 2012.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
Hilbert and Cohn-Vossen, Geometry and the Imagination. Chelsea Publishing Company. pag.278.
Robert C. Yates, 'A Handbook on curves and their properties', J.W.Edwards-Ann Arbor, 1947.
J.L. Coolidge, The Mathematics of great Amateurs. Second Edition. Claredon Press. Oxford. Jan de Witt's proof in page 124.
MORE LINKS

An Ellipsograph is a mechanical device used for drawing ellipses.
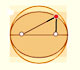
Every ellipse has two foci and if we add the distance between a point on the ellipse and these two foci we get a constant.
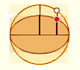
Transforming a circle we can get an ellipse (as Archimedes did to calculate its area). From the equation of a circle we can deduce the equation of an ellipse.

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.

We study different cylinders cut by an oblique plane. The section that we get is an ellipse.

Plane developments of cones cut by an oblique plane. The section is an ellipse.



 PREVIOUS
PREVIOUS


















 NEXT
NEXT