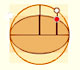
Archimedes got an ellipse shrinking a circle along one direction.
Then Archimedes could deduce the area of an ellipse as
a generalization of the area of a circle.
An ellipse has two axes of symmetry that we call the major and the minor axes.
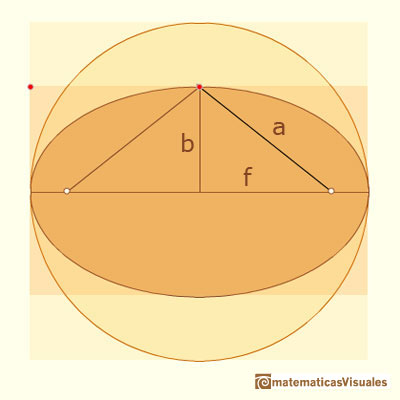
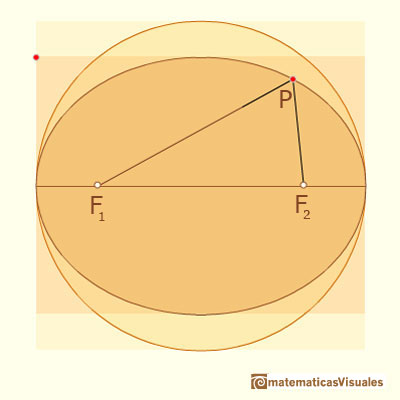
An ellipse is commonly defined as the locus of points P such that the sum of the distances
from P to two fixed points F1, F2 (called foci) are constant.
This two foci lies on its major axis, at equal distances from the center of the ellipse.
In this page we can see (intuitively) how Archimedes' approach and this definition of an ellipse are the same.
We might use Pythagoras' theorem to calculate the position of these two foci.
From the definition, a point P in the ellipse verify:
A circle is a special case of an ellipse (when a = b). In this case the two foci points are just the same: the center of the circle.
MORE LINKS
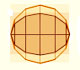
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.

An Ellipsograph is a mechanical device used for drawing ellipses.
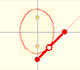
If a straight-line segment is moved in such a way that its extremities travel on two mutually perpendicular straight lines then the midpoint traces out a circle; every other point of the line traces out an ellipse.
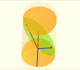
The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.

Durer was the first who published in german a method to draw ellipses as cone sections.

Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .
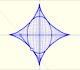
The Astroid is the envelope of a segment of constant length moving with its ends upon two perpendicular lines. It is also the envelope of a family of ellipses, the sum of whose axes is constant.
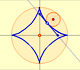
The Astroid is a particular case of a family of curves called hypocycloids.

We study different cylinders cut by an oblique plane. The section that we get is an ellipse.

Plane developments of cones cut by an oblique plane. The section is an ellipse.

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.
The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.

 NEXT
NEXT
 PREVIOUS
PREVIOUS