The Complex Cosine Function: a geometric approach
|
|
|
The real cosine function can be extended using the exponential function:
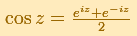
Since the exponential function is periodic with period
,
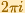it follows that the cosine function is periodic, but with period
.
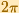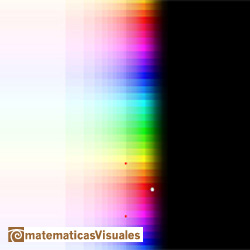
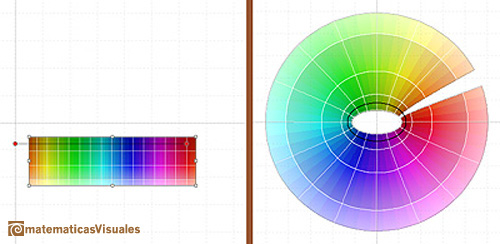
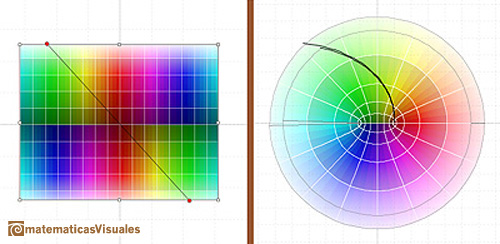
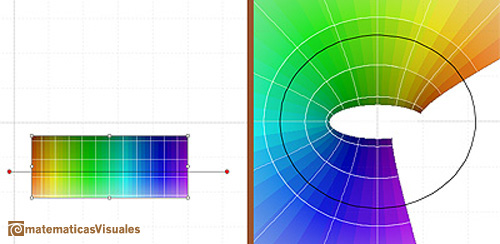
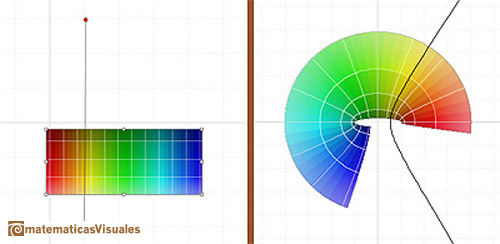
Dragging the rectangle we can see how the cosine function is periodic.
We can see another point of view of this periodicity in the page about the Taylor's Polynomial of the Cosine Function
The Complex Cosine Function have much in common with his real ancestors, por example:
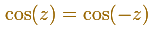
The image of a horizontal line is an ellipse:
The image of a vertical line is an hyperbola:
REFERENCES
Tristan Needham - Visual Complex Analysis. (pag. 88-89) - Oxford University Press
LINKS
The Complex Cosine Function maps horizontal lines to confocal ellipses.
The power series of the Cosine Function converges everywhere in the complex plane.
The Complex Exponential Function extends the Real Exponential Function to the complex plane.
By increasing the degree, Taylor polynomial approximates the sine function more and more.
Inversion is a plane transformation that transform straight lines and circles in straight lines and circles.
The usual definition of a function is restrictive. We may broaden the definition of a function to allow f(z) to have many differente values for a single value of z. In this case f is called a many-valued function or a multifunction.
Examples of complex functions: polynomials, rationals and Moebius Transformations.