The complex Exponential Function is the complex function that we can define as a power series and that extends
the real Exponential function to complex values
This series converges everywhere in the complex plane.
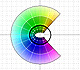
In this page we try to show the geometric nature of the mapping
The Exponential Function verifies
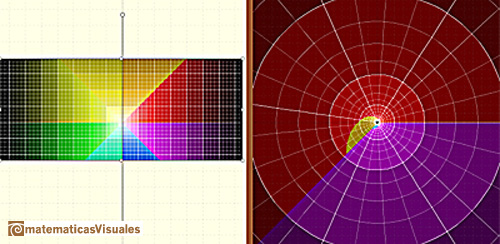
The Exponential Function es periodic with period 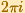 .
.
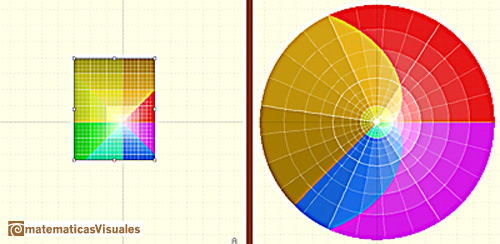
The entiry w-plane (with the exception of the origin) will be filled by the image of any horizontal strip in the
z-plante of height 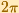 .
.
A line is mapped to a spiral (or to a line or to a circle).
Euler's formula
can be interpreted as saying that the Exponential Function "wraps the imaginary axis round and round the unit circle like a piece of string" (Tristan Needham).
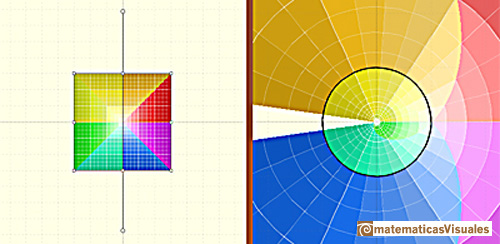
The half-plane to the left of the imaginary axis is mapped to the interior of the unit circle, and the
half-plane to the right of the imaginary axis is mapped to the exterior of the unit circle (Tristan Needham).
The images of the small squares closely resemble squares and (related to this) any two intersecting lines
map to curves that intersect at the same angle as the lines themselves (Tristan Needham).
MORE LINKS

Complex power functions with natural exponent have a zero (or root) of multiplicity n in the origin.

A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.

A complex polinomial of degree 3 has three roots or zeros.

Every complex polynomial of degree n has n zeros or roots.

Every complex polynomial of degree n has n zeros or roots.

Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.

The Complex Cosine Function maps horizontal lines to confocal ellipses.
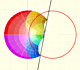
Inversion is a plane transformation that transform straight lines and circles in straight lines and circles.

Inversion preserves the magnitud of angles but the sense is reversed. Orthogonal circles are mapped into orthogonal circles

The usual definition of a function is restrictive. We may broaden the definition of a function to allow f(z) to have many differente values for a single value of z. In this case f is called a many-valued function or a multifunction.
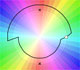
Multifunctions can have more than one branch point. In this page we can see a two-valued multifunction with two branch points.

The complex exponential function is periodic. His power series converges everywhere in the complex plane.

The power series of the Cosine Function converges everywhere in the complex plane.

We will see how Taylor polynomials approximate the function inside its circle of convergence.
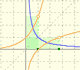
After the definition of the natural logarithm function as an integral you can define the exponential function as the inverse function of the logarithm.
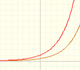
We can study several properties of exponential functions, their derivatives and an introduction to the number e.

By increasing the degree, Taylor polynomial approximates the exponential function more and more.

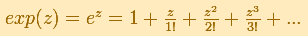
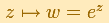
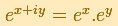
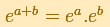
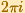 .
.
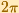 .
.
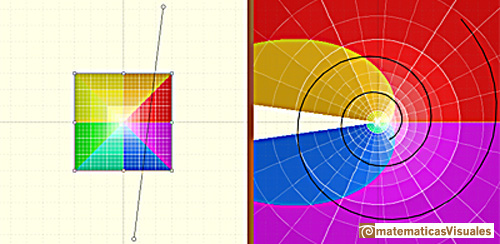
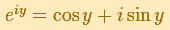
 NEXT
NEXT
 PREVIOUS
PREVIOUS