Felix Klein started his chapter about Taylor's Theorem writing: "I shall depart, namely, from de usual treatment in the textbooks by bringing to the foreground the finite series, so important in practice, and by ading the intuitive grasp of the situation by means of graphs. In this way it will all seem elementary and easily comprehensible."

"We begin with the question whether we can make a suitable approximation to an arbitrary curve y = f(x), for a short distance, by means of curves of the simplest kind." (Klein, 'Elementary Mathematics from an Advanced Standpoint' p.223)

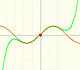
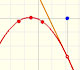
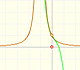
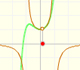
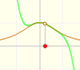
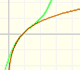
These approximations can be made using polynomials of increasing degrees, starting with the rectilinear tangent.

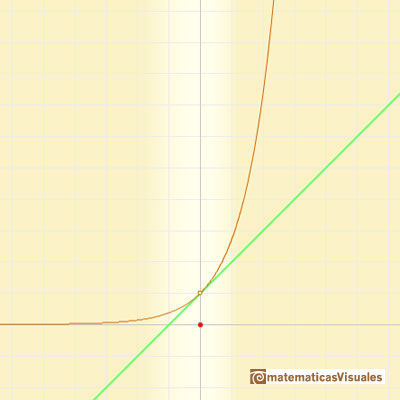
We can obtain better approximations using parabolas of second, third,... order.

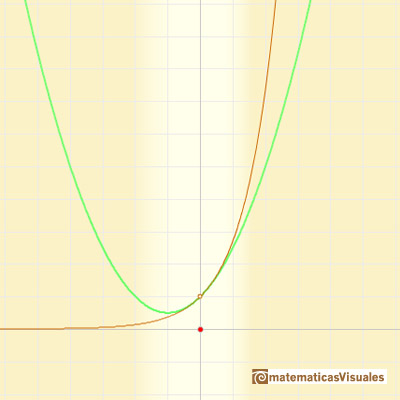
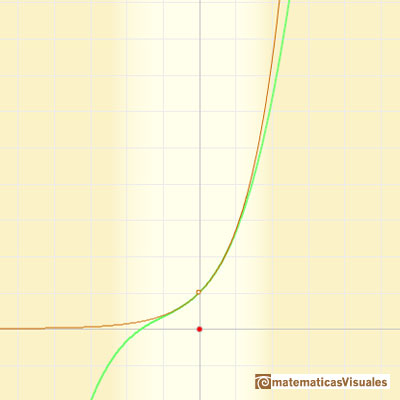
They are easy to calculate and approximates the curve arround a point (we call these polynomials 'parabolas of osculation' because they lie as close as possible to the curve). "Thus the quadratic parabola will coincide with y=f(x) not only in its ordinate but also in its first and second derivative (i.e., it will 'osculate')." (Klein, p. 224) These polynomials are known as Taylor polynomials and are obtained by considering the first terms of Taylor's series.

We have to investigate whether and how far these polynomials represent usable curves of approximation.

"The first question here is the extremely important one in practice as to the closeness with the n-th parabola of osculation represents the original curve. This implies an estimate of the remainder for the values of the ordinate, and is connected naturally with the passage of n to infinity. Can the curve be represented exactly, at least for a part of its couse, by an infinite power series?" (Klein, p. 226)

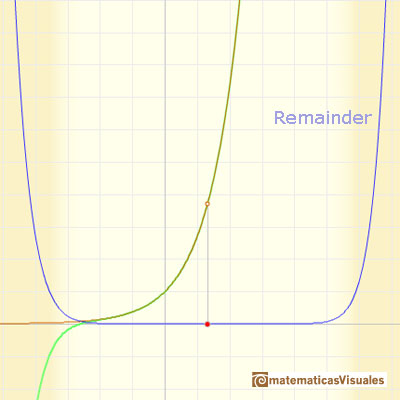
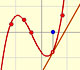
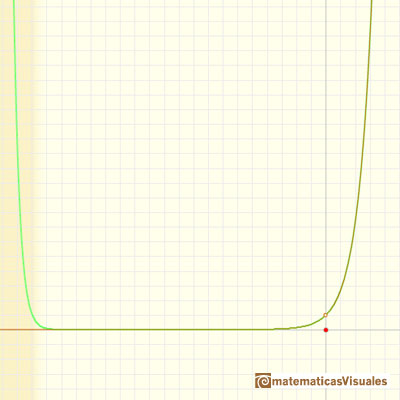
In the case of the exponential function, as the order increases, the parabolas give usable approximation to the original curve for a greater and greater interval. This is a wonderful behavior. We say then that the infinite series converge for all values of x.

The same is true for other functions, for example, the Sine Function. But it is not always the case.

Taylor's series of the exponential function at x=0 is:

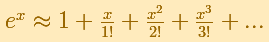
To understand better these power series we can investigate it in the Complex Plane, for example, Taylor polynomials: Complex Exponential Function.

REFERENCES

MORE LINKS

Taylor polynomials: Complex Exponential Function

The complex exponential function is periodic. His power series converges everywhere in the complex plane.

Taylor polynomials (3): Square root

The function is not defined for values less than -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials (4): Rational function 1

The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials (5): Rational function 2

The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials (6): Rational function with two real singularities

This function has two real singularities at -1 and 1. Taylor polynomials approximate the function in an interval centered at the center of the series. Its radius is the distance to the nearest singularity.

Taylor polynomials (7): Rational function without real singularities

This is a continuos function and has no real singularities. However, the Taylor series approximates the function only in an interval. To understand this behavior we should consider a complex function.

Mercator and Euler: Logarithm Function

Mercator published his famous series for the Logarithm Function in 1668. Euler discovered a practical series to calculate.

The Complex Exponential Function

The Complex Exponential Function extends the Real Exponential Function to the complex plane.

Polynomial functions and derivative (1): Linear functions

The derivative of a lineal function is a constant function.

Polynomial functions and derivative (2): Quadratic functions

The derivative of a quadratic function is a linear function, it is to say, a straight line.

Polynomial functions and derivative (3): Cubic functions

The derivative of a cubic function is a quadratic function, a parabola.

Polynomial functions and derivative (4): Lagrange polynomials (General polynomial functions)

Lagrange polynomials are polynomials that pases through n given points. We use Lagrange polynomials to explore a general polynomial function and its derivative.