The function

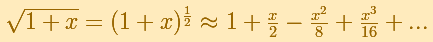
if different from the Exponential function or the Sine function because this function is not defined for all values (its domain is not the whole real line), then it has no sense to say that a polynomial approaches the function for all values of x or that the power series converges for all values of x.

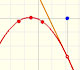
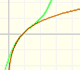
We can calculate the Taylor's series at x=0 easily, using Newton's Binomial Theorem, but the function is not defined when x is smaller than -1.

Then our interest is to study what happens when x is greater or equal to -1.

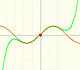
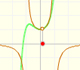
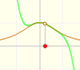
"In the interval (-1, +1) the parabolas approach the original curve more and more as the order increases; but to the right of x = 1 they deviate from it increasingly, now above, now below, in a striking way." (Felix Klein)

We call this interval (-1, +1) 'circle of convergence' of the power series. It is a typical behavior that a power series converges inside the circle of convergence and diverges outside. We understand better the use of the word 'circle' when we go to the Complex Plane.

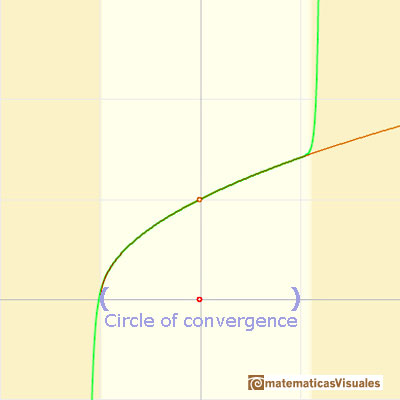
It is interesting to study what happens at the 'border' points. At the point x = -1, the branch of the original curve which appears in the drawing ends at a vertical tangent, "all the parabolas extends beyond this point but approach the original curve more and more at x = -1, by becoming ever steeper". At the point x = +1, symmetrical to x = -1, the parabolas approach the original curve more and more closely too.

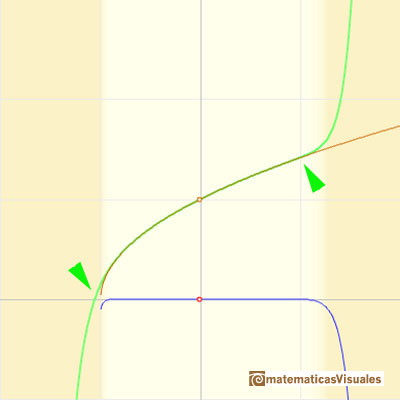
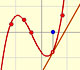
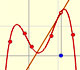
We can see what happens with some functions with singularities, for example, Taylor polynomials (4): Rational function 1."

REFERENCES

MORE LINKS

Taylor polynomials (5): Rational function 2

The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials (6): Rational function with two real singularities

This function has two real singularities at -1 and 1. Taylor polynomials approximate the function in an interval centered at the center of the series. Its radius is the distance to the nearest singularity.

Taylor polynomials (7): Rational function without real singularities

This is a continuos function and has no real singularities. However, the Taylor series approximates the function only in an interval. To understand this behavior we should consider a complex function.

Mercator and Euler: Logarithm Function

Mercator published his famous series for the Logarithm Function in 1668. Euler discovered a practical series to calculate.

Taylor polynomials (1): Exponential function

By increasing the degree, Taylor polynomial approximates the exponential function more and more.

Multifunctions: Powers with fractional exponent

The usual definition of a function is restrictive. We may broaden the definition of a function to allow f(z) to have many differente values for a single value of z. In this case f is called a many-valued function or a multifunction.

Polynomial functions and derivative (1): Linear functions

The derivative of a lineal function is a constant function.

Polynomial functions and derivative (2): Quadratic functions

The derivative of a quadratic function is a linear function, it is to say, a straight line.

Polynomial functions and derivative (3): Cubic functions

The derivative of a cubic function is a quadratic function, a parabola.

Polynomial functions and derivative (4): Lagrange polynomials (General polynomial functions)

Lagrange polynomials are polynomials that pases through n given points. We use Lagrange polynomials to explore a general polynomial function and its derivative.