The usual definition of a function is restrictive. We may broaden the definition of a function to allow f(z) to have many differente values for a single value of z. In this case f is called a "many-valued function" or a multifunction.

For example, we know that

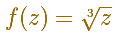
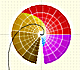
has three different values (if z is not zero), so it is a three-valued multifunction.

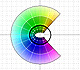
In this case, we see that each color is shown three times and that each z value has three different images with the same module but different argument.

If we arbitrarily choose one of the three images of a given point z and gradually moves away from this initial position then the image moves away in a completely determined way -its distance from the origin is the cube root of the distance of z, and its angular speed is one third that of z. (Needham, p.91)

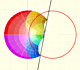
As z travels along a closed loop like in this picture, its image f(z) travels along a closed loop and returns to its original value.

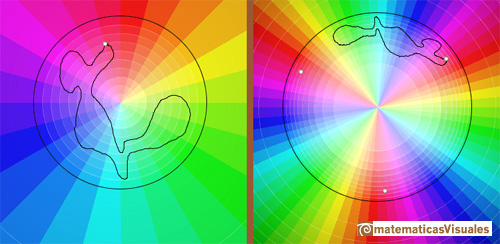
However, if z instead travels along a closed loop which goes round the origin once, then f(z) does not return to its original value but instead ends up at a different cube root. Note that the detailed shape of the loop is irrelevant, all that matters is that it encircles the origin once. (Needham, p.91)

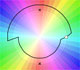
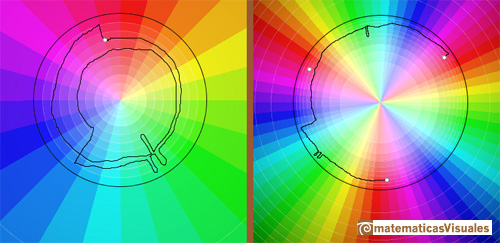
Similarly, if z travels along a closed loop encircling the origin twice, then f(z) ends up at the third and final cube root. (Needham, p.91)

Clearly, if z travels along a loop that encircled the origin three times, then f(z) returns to its original root. (Needham, p.91)

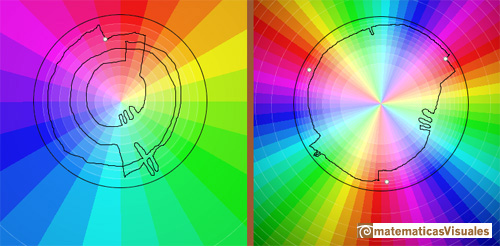
The point z = 0 is called a branch point of the multifunction f(z).

MORE LINKS

Complex Polynomial Functions(1): Powers with natural exponent

Complex power functions with natural exponent have a zero (or root) of multiplicity n in the origin.

Complex Polynomial Functions(2): Polynomial of degree 2

A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.

Complex Polynomial Functions(3): Polynomial of degree 3

A complex polinomial of degree 3 has three roots or zeros.

Complex Polynomial Functions(4): Polynomial of degree n

Every complex polynomial of degree n has n zeros or roots.

Complex Polynomial Functions(5): Polynomial of degree n (variant)

Every complex polynomial of degree n has n zeros or roots.

Cero and polo (Spanish)

Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.

Cero and polo (variant) (Spanish)

The Complex Exponential Function

The Complex Exponential Function extends the Real Exponential Function to the complex plane.

The Complex Cosine Function

The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.

The Complex Cosine Function: mapping an horizontal line

The Complex Cosine Function maps horizontal lines to confocal ellipses.

Inversion

Inversion is a plane transformation that transform straight lines and circles in straight lines and circles.

Taylor polynomials: Complex Exponential Function

The complex exponential function is periodic. His power series converges everywhere in the complex plane.

Taylor polynomials: Complex Cosine Function

The power series of the Cosine Function converges everywhere in the complex plane.

Taylor polynomials: Rational function with two complex singularities

We will see how Taylor polynomials approximate the function inside its circle of convergence.