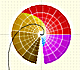
|
|
|
Complex Polynomial Functions (1): Powers
Power Complex Functions with exponent a whole number
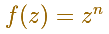
have a zero (also called a root) of multiplicity n at 0 (the origin). They are simple examples of polynomial functions.
This representation allow us to see how at a zero of multiplicity n the color cycle goes round the zero n times.
You can change the value of n (the exponent) to see the representation of different power funtions.
The identity function has a zero of multiplicity 1:
The power function of degre 2 has a zero of multiplicity 2:
The power function of degre 3 has a zero of multiplicity 3:
The power function of degre 4 has a zero of multiplicity 4:
The power function of degre 5 has a zero of multiplicity 5:
REFERENCES
Tristan Needham - Visual Complex Analysis. Oxford University Press.
NEXT
A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.
MORE LINKS
A complex polinomial of degree 3 has three roots or zeros.
Every complex polynomial of degree n has n zeros or roots.
Every complex polynomial of degree n has n zeros or roots.
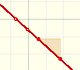
Two points determine a stright line. As a function we call it a linear function. We can see the slope of a line and how we can get the equation of a line through two points. We study also the x-intercept and the y-intercept of a linear equation.
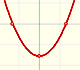
Polynomials of degree 2 are quadratic functions. Their graphs are parabolas. To find the x-intercepts we have to solve a quadratic equation. The vertex of a parabola is a maximum of minimum of the function.
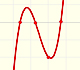
Polynomials of degree 3 are cubic functions. A real cubic function always crosses the x-axis at least once.
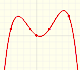
We can consider the polynomial function that passes through a series of points of the plane. This is an interpolation problem that is solved here using the Lagrange interpolating polynomial.
Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.
Una primera aproximación a estas transformaciones. Representación de dos haces coaxiales de circunferencias ortogonales.
The Complex Exponential Function extends the Real Exponential Function to the complex plane.
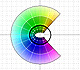
The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.
The Complex Cosine Function maps horizontal lines to confocal ellipses.
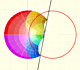
Inversion is a plane transformation that transform straight lines and circles in straight lines and circles.
Inversion preserves the magnitud of angles but the sense is reversed. Orthogonal circles are mapped into orthogonal circles
The usual definition of a function is restrictive. We may broaden the definition of a function to allow f(z) to have many differente values for a single value of z. In this case f is called a many-valued function or a multifunction.
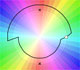
Multifunctions can have more than one branch point. In this page we can see a two-valued multifunction with two branch points.
The complex exponential function is periodic. His power series converges everywhere in the complex plane.
The power series of the Cosine Function converges everywhere in the complex plane.
We will see how Taylor polynomials approximate the function inside its circle of convergence.