Inversion is a one-to-one transformation of the points of the plane (except one point) by means of a given circle (circle of inversion).
We shall call this circle C, of radius r and centre q. The center of the circle of inversion (center of inversion) has no image.
If the center of the circle of inversion is the origin and the radius is 1 this transformation has a simple formula:
In the general case, this mapping is given by:
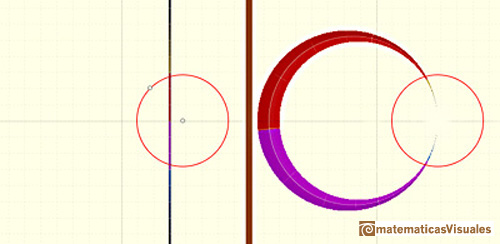
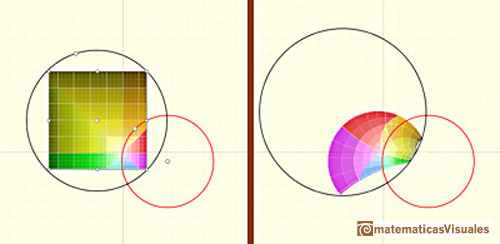
The points on the circle of inversion transform into themselves and each point inside the circle is transformed to a
point outside the circle (and vice-versa). Each point, its image and the center of the circle of inversion are in the
same line. Sometimes we call this transformation as reflection in a circle.
Each line through the center of inversion is transformed in the same line.
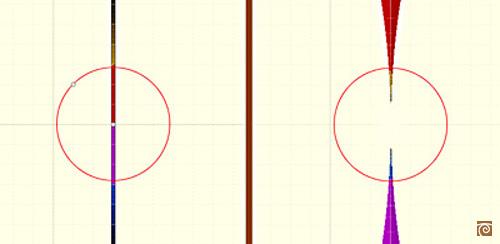
Each line not passing through the center of inversion is transformed in a circle through the center of inversion.
The inverse of a circle is a straight line or a circle. It is a line if the circle passes through the center of inversion.
The image of a circle not passing through the center of inversion is another circle not passing through the center
of inversion.
REFERENCES
Hilber and Cohn-Vossen - Geometry and the Imagination (pag. 253) - Chelsea Publishing Company
Coxeter - Introduction to Geometry - Wiley and Sons.
Pedoe - Circles, a Mathematical View - Dover
Rademacher and Toeplitz - The Enjoyment of Mathematics
Ogilvy - Excursions in Geometry (pag. 24)- Oxford University Press
MORE LINKS

Complex power functions with natural exponent have a zero (or root) of multiplicity n in the origin.

A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.

A complex polinomial of degree 3 has three roots or zeros.

Every complex polynomial of degree n has n zeros or roots.

Every complex polynomial of degree n has n zeros or roots.

Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.
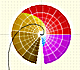
The Complex Exponential Function extends the Real Exponential Function to the complex plane.
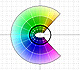
The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.

The usual definition of a function is restrictive. We may broaden the definition of a function to allow f(z) to have many differente values for a single value of z. In this case f is called a many-valued function or a multifunction.
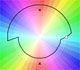
Multifunctions can have more than one branch point. In this page we can see a two-valued multifunction with two branch points.

The complex exponential function is periodic. His power series converges everywhere in the complex plane.

The power series of the Cosine Function converges everywhere in the complex plane.

We will see how Taylor polynomials approximate the function inside its circle of convergence.

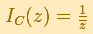
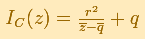
 NEXT
NEXT




















 PREVIOUS
PREVIOUS








