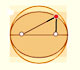
We have already studied the Ellipsograph or "Trammel of Archimedes". It is a device that consists of a rod that is moving with two fixed points upon two fixed perpendicular lines.
We know that every point on this rod draws an ellipse.
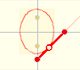
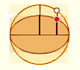
If we consider the envelope of this lines of constant length moving with its ends upon two perpendicular lines ("sliding ladder") the result is a curve that has four cups. Its name is Astroid.
The Astroid is also the envelopè of a family of ellipses, the sum of whose axes is constant (the length of the moving segment).
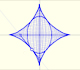
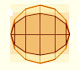
An astroid is defined as the locus of a point P on the circunference of a circle that rolls without slipping inside a larger circle of radius four times as large.
Then the astroid is a kind of hypocycloid. A hypocycloid is a plane curve generated by a fixed point on a small circle that rolls within a large circle.
If the smaller circle has radius r, and the larger circle has radius 4r the curve has four cups. It seems equal to the envelope of the sliding ladder. But, it is the same curve? We need to prove it (following Apostol and Mnatsakanian).
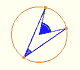
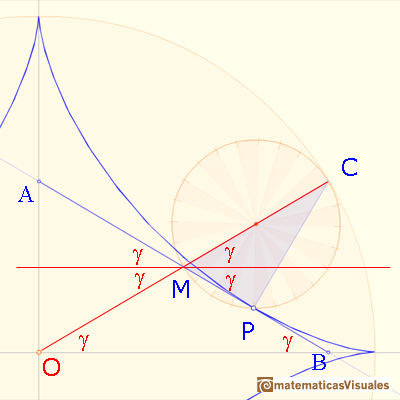
The point P rolls without slipping. The two circular arcs CL and CP have equal lengths because the smaller circle rolls along the larger. The central angle of the smaller circle is four times the central angle of the larger circle (because the radius of the larger circle is four times the radius of the smaller one).
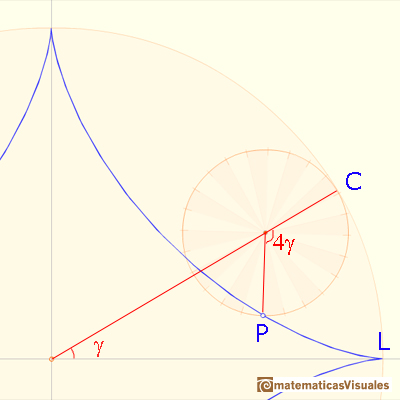
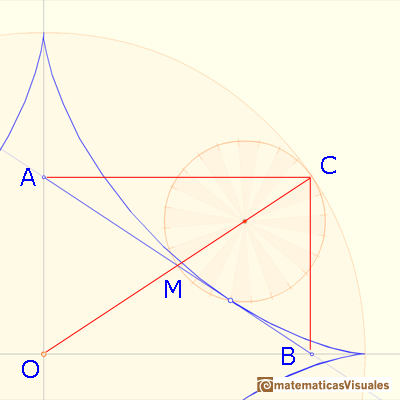
How can we draw the tangent to the astroid through P?. We want to probe that segment AB has a fixed length. If we show that the length of AB doesn't change as P moves along the astroid, this will show that AB is a trammel.
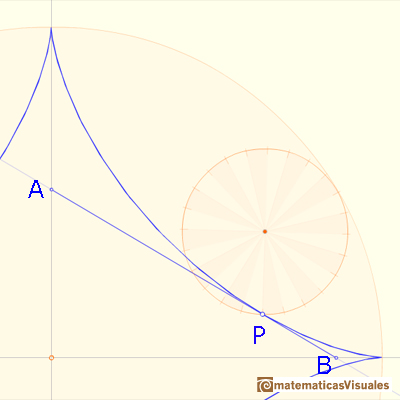
M is the midpoint of OC. The line AB drawn through PM, perpendicular to CP, is algo tangent to the astroid at P because C is the center of instantanteous rotation of the smaller circle as it rolls inside the larger circle.
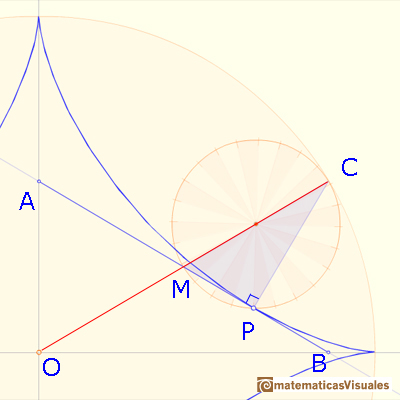
To prove that the length of AB doesn't change as P moves along the astroid we can show that M is also the midpoint of AB, and that the triangle OMA is isosceles.
Using the properties of the central and inscribed angles:
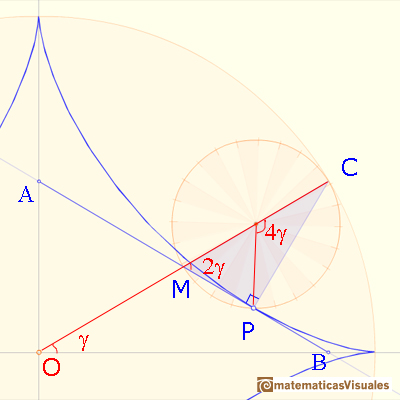
An horizontal line through M bisects angle CMA as shown:
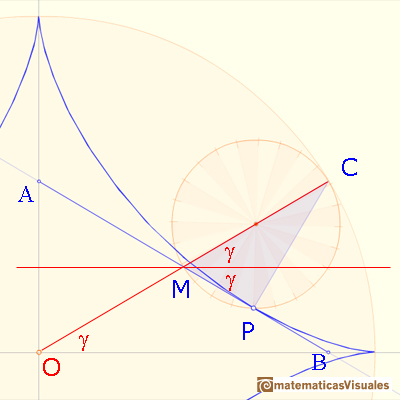
Then the triangle OMB is isosceles:
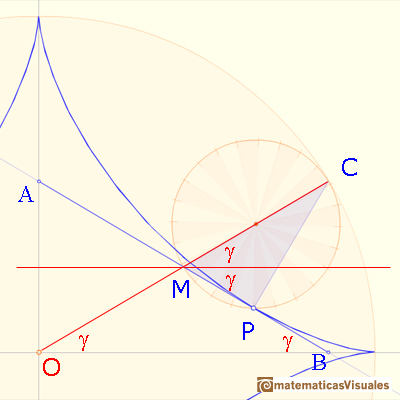
Triangle OMA is isosceles too. Then AB has fixed length, so it is a trammel, and we have already seen that it is always tangent to the astroid.
"The envelope of a moving trammel of fixed length is an astroid". (Apostol and Mnatsakanian)
REFERENCES
 PREVIOUS
PREVIOUS
MORE LINKS