Albrecht Dürer (1471-1528) was a German painter and engraver. In 1525 Dürer published the first mathematical book in German, the "Four Books on Measurement" or "Course in the Art of Measurement with Compass and Ruler". (Underweysung der Messung mit dem Zirckel und Richtscheyt).
One of the most interesting features of the First Book is the first discussion in German of conic sections.
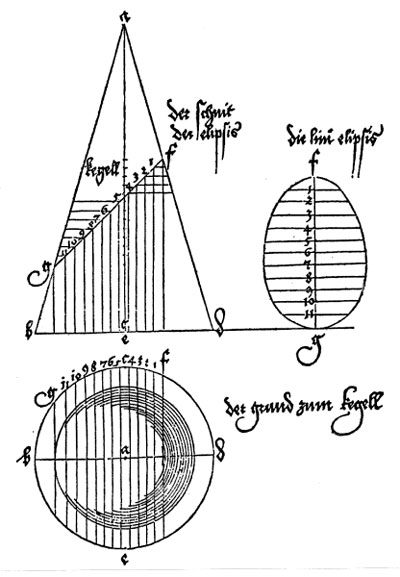
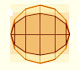
His beautiful and original method uses a side view and a view from above of a cone cut by an oblique plane.
DISCUSSION
Some publications accuse Dürer of having made big mistakes drawing ellipses. Here we can read two opinions defending Dürer's work. These points of view are more balance and well documented.
Dan Pedoe wrote: "The ellipse shown is egg-shaped, whereas a true ellipse has two axes of symmetry. It has been thought that Dürer, like any schoolboy, felt that an ellipse was bound to widen with the widening of the cone of which it is a section, and Kepler, a hundred years later, was amused by this apparent error, although much impressed with Dürer's work. Dürer, wishing to find a German word for ellipsis, did coin the word Eierlinie, egg-line, but on the other hand if one repeats the construction, a minute error will produce the egg-shape effect, and I am not convinced that Dürer was misled. It was Kepler, by the way, who first determined that the orbits of the planets are ellipses, and not epicycles, and can therefore be said to have established the ellipse as a fundamental curve." (Dan Pedoe, Geometry and the Visual Arts)
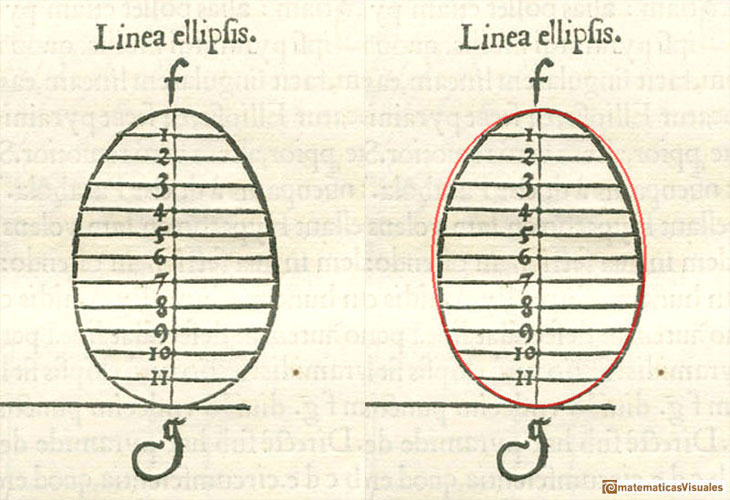
Dirk Huylebrouck makes a strong defense of Dürer in front of the accusations that he would have drawn erroneous curves. "The sole valid arguments of the critics, is Dürer's drawing on page 30 of his book 'Underweysung der Messung' or 'Teaching Measurements' (Nürnberg, 1525). It shows a drawing for the plane intersection of a cone. It would become a classic in all courses on Monge's projection method. In this drawing the ellipse is indeed slightly wider where the cone is wider. The critics state that Dürer made 'an elaborate technique to accurately draw the ellipse', but anyone who followed descriptive geometry in high school would laugh away the adjetive 'elaborate'. The logic of the method is simple, but the execution is more problematic. In fact, anyone who ever made this drawing with compass, ruler and pencil experienced it is not so easy get a smooth ellipse. One easily gets and egg shape or else an ellipse with sharp vertices on the longer axis. (...) Knowing the techniques and materials at his disposal, his drawings surely was good enough for any teacher of Monge geometry. It looks slightly like an egg, sure, but it is not exaggeratedly wrong. (...) Perhaps we are too spoiled today by computer drawings to undertand the technical difficulties when making such a drawing by hand".
He wrote that "there is no proof at all Dürer thought an elliptic intersection gets broader where the cone gets broader. He never said so".
Now we are going to prove that the minor axis of an ellipse is a symmetry axis.
INVESTIGATE
Try to prove this result before continuing reading. We need only basic Mathematics to do that.
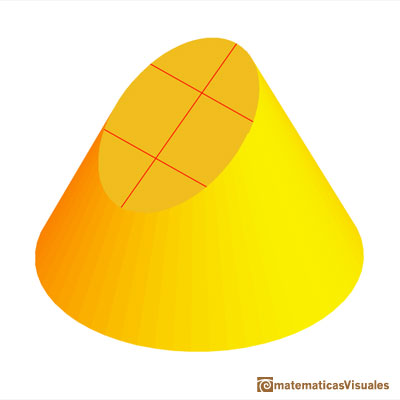
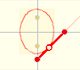
First, for each point on the major axis we need to calculate k, how wide is the ellipse at this point.
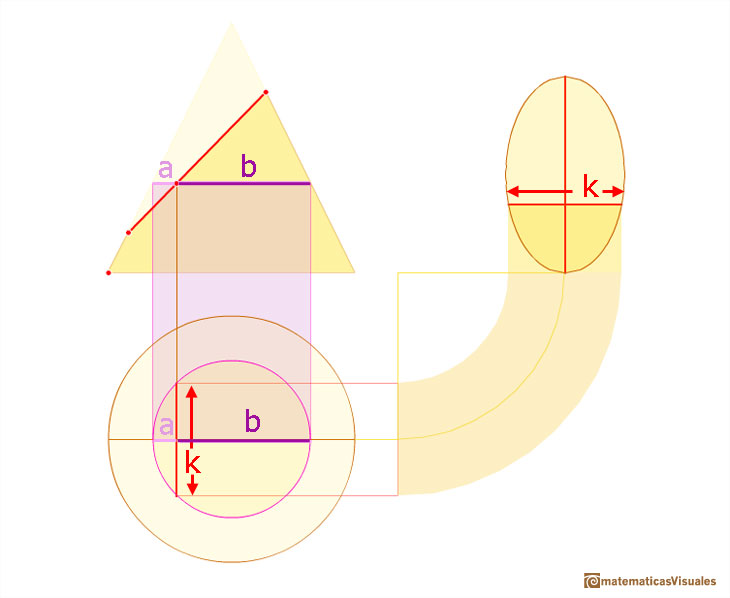
It could be useful to review the geometric mean of two numbers. I used this idea when we studied the sphere.
Now, we consider two symmetric points on the major axis of the ellipse.
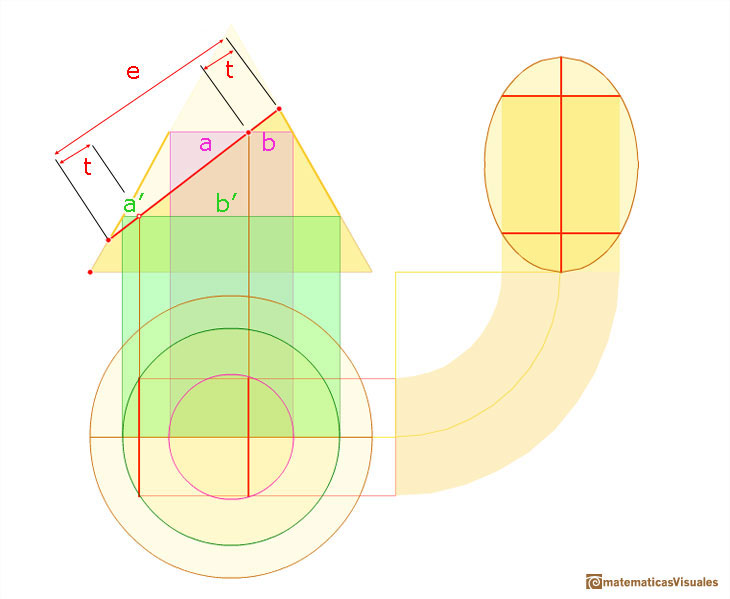
We must prove that
Or, simply
In the next image there are highlighted two similar triangles.
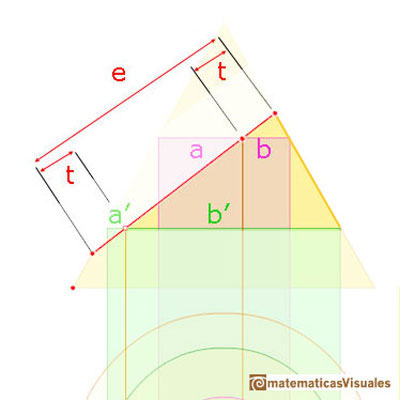
Then
Here we can see two more similar triangles.
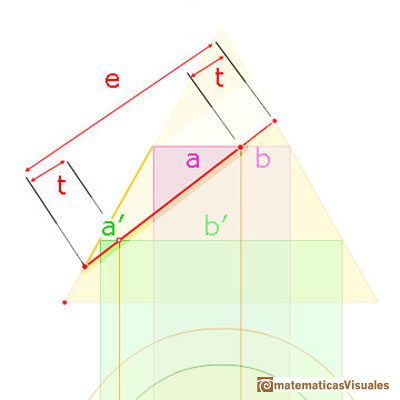
And we can write
Mixing these two equalities
And then
This is what we wanted to prove.
REFERENCES
MORE LINKS

















 NEXT
NEXT

 PREVIOUS
PREVIOUS