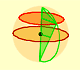
We are going to study a projection from the sphere to the cylinder. This is a kind of perspective cylindrical projection. Each point on the sphere is projected horizontally onto a cylinder tangent to the sphere. It is an equal-area projection that was first rigorously defined by Johann H. Lambert (1772).
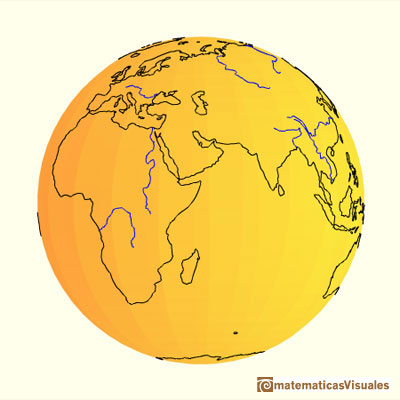
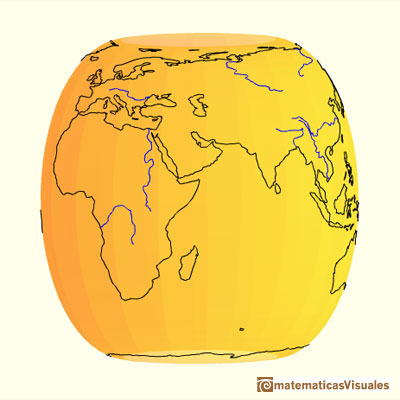
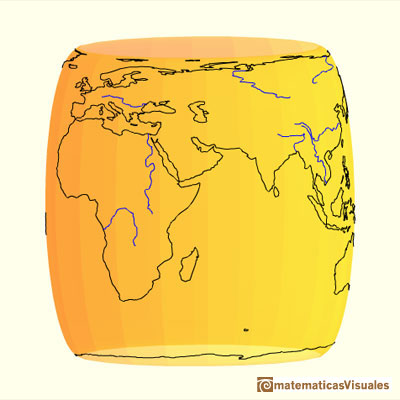
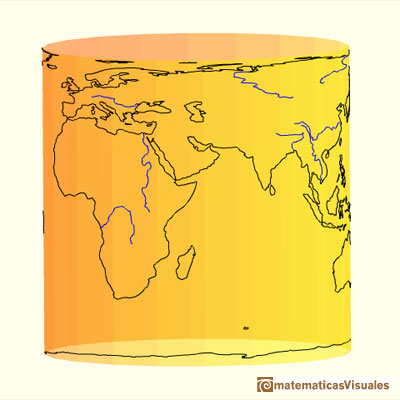
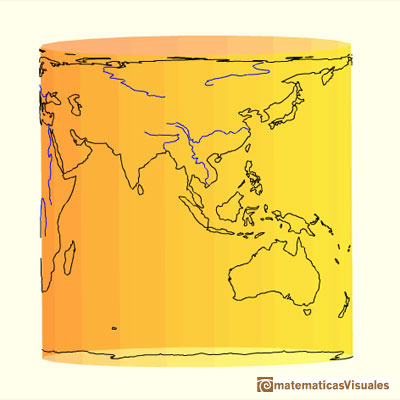
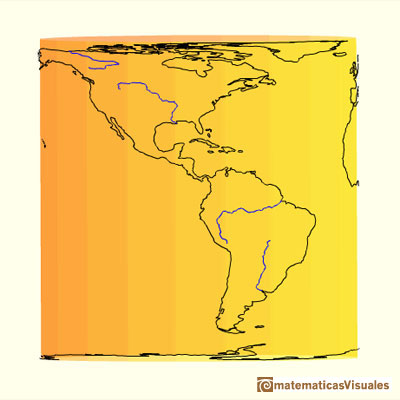
Hugo Steinhaus wrote about this projection:
"If we place a sphere in a cylinder touching it along the Equator, and if we project the sphere on the cylindrical surface by prolonging the planes of every parallel to cut the cylinder and do the same with all the meridian planes, we get on the cylinder a map of the sphere. By cutting the cylinder open and laying it flat, we get a map of the sphere with a rectangular and straight net of meridians and parallels. This map has the peculiarity (known to Archimedes) of conserving areas. If we then imagine the sphere covered with a thin uniform layer of paint or clay and bring every particle of it to its proper place on the cylinder, we shall get a uniform covering of the cylinder with matter; if we transfer it horizontally back to the common axis of the cylinder and the sphere, we shall cover the axis uniformly with matter."
In his book 'On the Sphere and Cylinder', Archimedes demonstrated the formula for the surface area of a sphere.
This surface area is the same as the lateral surface area of the tangent cylinder and it is four times the surface area of a great circle in the sphere.



After that we can use an intuitive argument to deduce the volume of a sphere.
C.H.Edwards wrote:
"The relationship between V and the surface area S is sugested by a heuristic argument similar to the one in the discussion of the area and the circunference of a circle.

We regard the sphere as approximately the union of indefinitely many pyramids with the center of the sphere as their common vertex, and with their bases forming a polyhedral surface with indefinilety many faces inscribed in the sphere, each of which almost coincides with a small piece of the sphere.



Since the height of each of the pyramids will virtually equal the radius of the sphere, and the volume of a pyramid is one-third of the product of its height and its base, it seems evident that
Then we can derive V from S. Archimedes in his book 'The Method' followed the opposite direction and derived S from V.
Archimedes wrote in his book 'The Method':
"From the theorem that a sphere is four times as great as the cone with a great circle of the sphere as base and with height equal to the radius of the sphere I conceived the notion that the surface of any sphere is four times as great as a great circle in it: for, judging from the fact that any circle is equal to a triangle with base equal to the circumference and height equal to the radius of the circle, I apprehended that, in like manner, any sphere is equal to a cone with base equal to the surface of the sphere and height equal to the radius." (cited by Edwards)
Although in Kepler's times Archimedes' 'The Method' was lost, Kepler followed a very similar argument to deduce the surface area of a sphere.

Kepler wrote a book in 1615 about areas and volumes of surfaces and solids: Nova stereometria doliorum vinariorum (New solid geometry of wine barrels). In this book Kepler thought of the sphere as being composed of an infinite number of infinitesimal pyramids or cones each having its vertex at the center of the sphere and whose bases made up the surface of the sphere.
This is one example of a theorem about the sphere in one original Kepler's Nova stereometria doliorum vinariorum. We can read this page, and the full book, in The Posner Memorial Collection,Carnegie Mellon University Libraries.
A translation could be: The surface area of a sphere is four times the area of a great circle of the sphere.
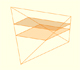
We can review the volume and the surface area of a cylinder circunscribed to a sphere of radius r:

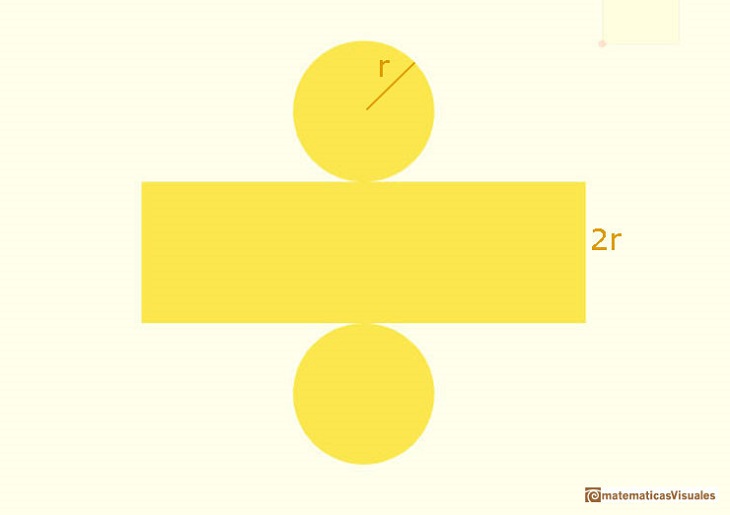
Then we can compare the surface area of an sphere and a cylinder:
And the volume of an sphere and a cylinder:
Then we can conclude:
The ratio of the surface areas of the sphere and the cylinder is the same as the ratio of their volumes.
Archimedes was very proud of these results and he requested that on his tombstone be carved a sphere inscribed in a right circular cylinder whose height equals its diameter.
REFERENCES
 PREVIOUS
PREVIOUS
MORE LINKS




















 NEXT
NEXT