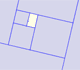
|
|
|
We start with a regular pentagon and we want to know the ratio between the diagonal and the side of the pentagon.
We can think that the side of the regular pentagon is 1. And the diagonal is represented by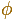 
, the Greek letter phi.
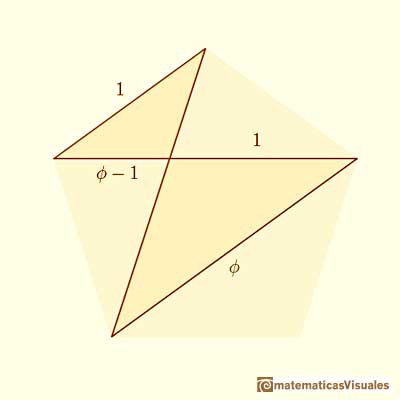
We have two homothetic isosceles triangles:
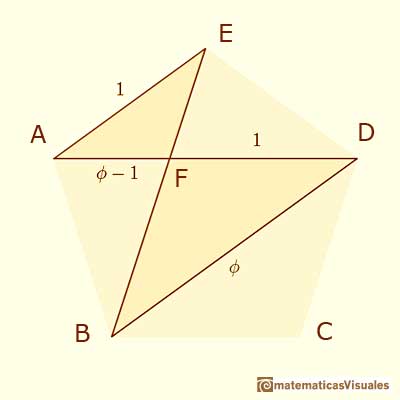
We can write a proportion:
Using the numbers 1 and :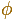
Hence 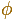is the positive root of the quadratic equation:
The value of 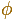is:
These are some basic properties of :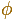
is called the golden ratio or the golden section.
We can say that the diagonal of a regular pentagon are in golden ratio to its sides.
The point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio (or "in extreme and mean ratio").
We suppose that Pythagoras and the Pythagoreans (around 500 BC) knew this ratio because their symbol was the pentagram (a pentagon with its diagonals) but the first written reference we have is in Euclid´s Elements (around 300 BC):
Book VI, Definition 3: "A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less". (For example, in Euclid's Elements at Clark University by D.E. Joyce)
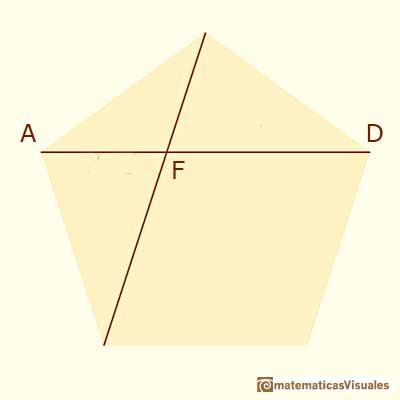
The first reference to this kind of construction appeared in Book II, Proposition 11. That was before ratios were defined and then the proposition is in terms of areas: "To cut a given straight line so that the rectangle contained by the whole and one of the segments equals the square of the remaining segment". (Euclid's Elements at Clark University by D.E. Joyce)
Using our notation:
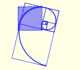
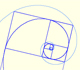
Usign the golden ratio we can draw a regular pentagon, a golden triangle and a golden rectangle and is related with the icosahedron and the dodecahedron.
With a strip of paper we can make a knot and get a pentagon and a pentagram:
Zome is a wonderful tool to play with the golden ratio:
Some examples of pentagonal symmetry:
REFERENCES
NEXT
MORE LINKS
