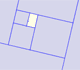
|
|
|
Dilative Rotations or Spiral Similarities are particular cases of transformations that we call similarities.
Similarities are transformations that change each figure into a similar figure, preserving angles, "though it may alter distances. However, all distances are increased (or decreased) in the same ratio, called the ratio of magnification" (Coxeter and Greitzer, p.94)
In video and images we are using one classical illustration from Alice's Adventures in Wonderland, drawn by John Tenniel.
If similarities preserve distances they are isometries or congruent transformations. Isometries transform each figure into a congruent figure. Similarities include, as special cases, isometries.
The simplest isometry is a translation.
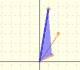
A rotation is a similarity that is also an isometry:
"The simplest kind of similarity is a dilatation [also called dilation], which transform each line into a parallel line. Any dilatation that is not merely a translation is called a central dilatation, because all the lines joining corresponding points of the figure and its image are concurrent." (Coxeter and Greitzer, p.94)
Half-turns are isometries that can be seen as rotations or central dilatations:
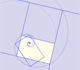
Central dilatations have an invariant point and it is true that any dilatation that is not a translation has an unique invariant point (see Coxeter, p. 69).
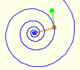
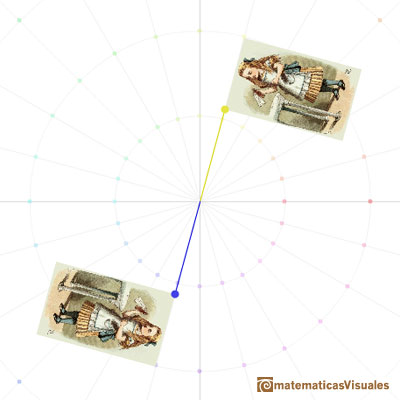
The combination of a central dilatation and a rotation about the same center is called a dilatative rotation or spiral similarity.
In the next video you can see a dilative rotation as a continuous transformation: first, rotation, then, dilatation.
Dilative rotations are also called Spiral Similarities. In the next applet you can see a continuous transformation that is following the path of an equiangular spiral.
REFERENCES
NEXT
PREVIOUS
MORE LINKS
