The origin of complex numbers is related with the solution of the cubic equation (Cardano, in 1545, Bombelli, in 1572). (Not from the study of quadratic equations) [For a very interesting historical introduction, see Tristan Needham, (pag. 1-5), who refers to Stillwell]

Complex numbers include the real numbers and also such "imaginary" numbers such as the square root of -1.

If we accept complex numbers then all the polynomical equations with real (or complex) coefficients has roots or solutions (Fundamental Theorem of Algebra, by Gauss).

In particular

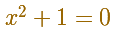
This is the symbol we use for the imaginary unit, the square root of -1. This symbol is due to Euler:

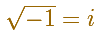
Then

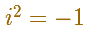
"Imaginary numbers made their own way into arithmetic calculations without the approval, and even against the desires of individual mathematicians, and obtained wider circulation only gradually and to the extent to which they showed themselves useful." (Klein, 56)

But, years later, "this discovery would ultimately have a profound impact on the whole of mathematics, unifiying much that had previously seemed disparate, and explaining much that had previously seemed inexplicable" (Needham, 1)

One important idea is the extension of the concept of number: "Beginning with the natural numbers such as 1 and 2, we proceed to the integers, then to the rational numbers, then to the real numbers, then to the complex numbers (and if we had time we could continue with hypercomplex numbers). Each stage is motivated to our desire to be able to solve a certain kind of equations." (Coxeter, 135)

"The nineteenth century finally brought the clear understanding of the nature of complex numbers. In the first place we must enphasize here the geometric interpretation to which various investigators were led about the end of the century. It will suffice if I mention the man who certainly went deepest into the essence of the thing and who exercised the most lasting influence upon the public, namely Gauss." (Klein, 56)

It is usual to start the study of complex numbers with a purely formal foundation which reduces them to dependence upon real numbers (definition, rules of addition, multiplication and division).

"Besides this purely formal treatment, we should of course like to have a geometric, or otherwise visual, interpretation of complex numbers and operations with them, in which we might see a graphical foundation of consistency. This is supplied by common geometric interpretation, which looks upon the totality of points (x,y) of the plane in an xy-coordinate system as representing the totality of complex numbers z = x + iy." (Klein, 57))

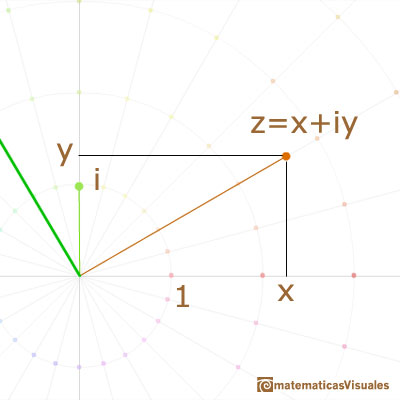
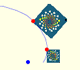
We call such representacion Argand diagram or Complex plane. It was formulated by C. Wessel (1797), rediscovered by J.R.Argand (1806), and rediscovered again by Gauss.

Since the real numbers occupy the whole x-axis, it is a natural extension to represent the complex numbers as points in the plane, vector from the origin or ordered pairs of real numbers.

The sum of two numbers follows the familiar parallelogram construction and is represented by a translation of the plane into itself. Points are added like the corresponding vectors from the origin.

Multiplication by a real number appears as a dilatatation.

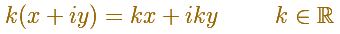
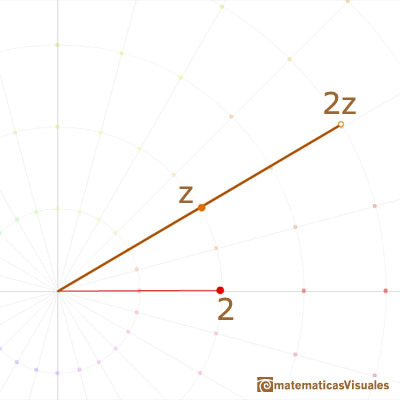
In particular, multiplication by -1 is the half-turn about O.

What, then, is multiplication by "the square root of -1"? This must be a transformation whose "square" is the half-turn about O. The obvious answer is a quater-turn about O. A right angle positive or counterclockwise rotation.

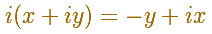
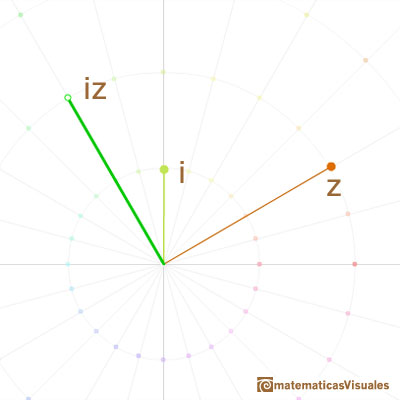
Following algebraic rules we can get the formula for the multiplication of two complex numbers:

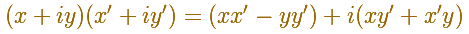
But, what is the geometric meaning of the multiplication of two complex numbers?

Multiplication by an arbitrary complex number should be a transformation which leaves 0 invariant and includes both dilatations and rotations as special cases. The obvious transformation of this kind is a dilatative rotation. Accordingly, the operation of multiplying the general point (x, y) by any particular point (a, b) is defined to the dilative rotation (with center 0) that transform (1,0) into (a, b).

Dilative rotation

A Dilative Rotation is a combination of a rotation an a dilatation from the same point.

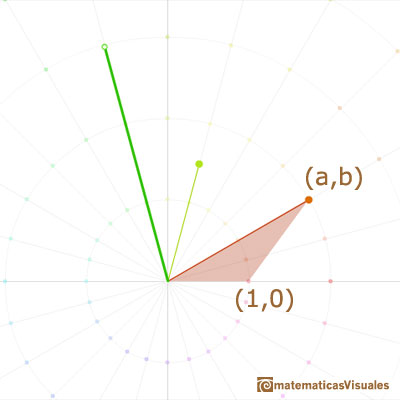
Multiplication is a similarity transformation, i.e., turning and stretching (the origin remaining fixed).

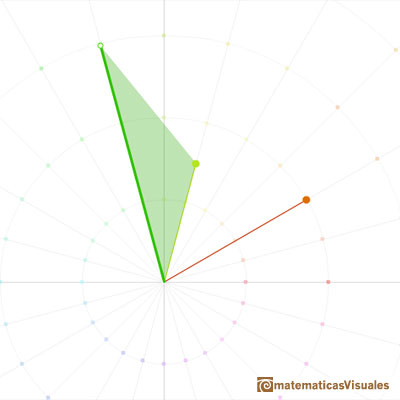
Turning (rotation) ...

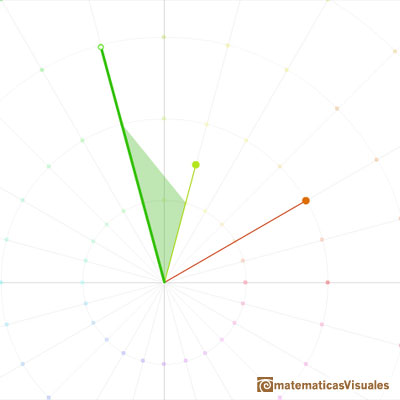
stretching (dilatation).

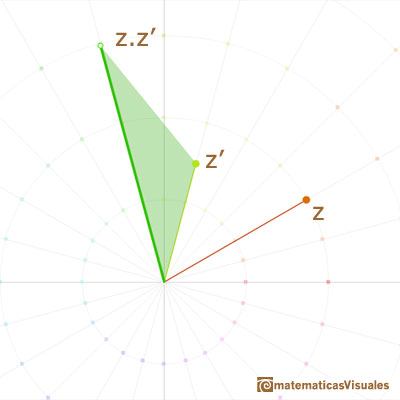
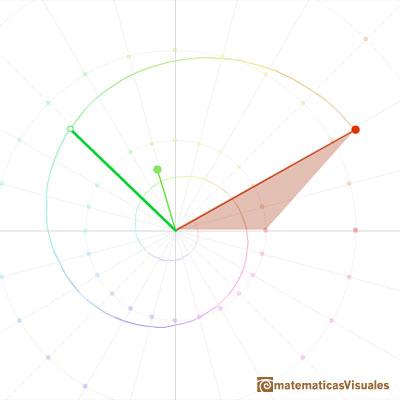
It is better to use polar coordinates. The polar coordinates of a complex number are given by its distance from the origin 0 (length or module) and its angle (argument).

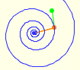
Then we can get the result of multiplying two complex numbers adding their angles (arguments) and multiplying their lengths (modules).

In the next representation we want to show the multiplication of two complex numbers as a continuous dilative rotation using an animation.

Equiangular spiral

In an equiangular spiral the angle between the position vector and the tangent is constant.

Klein insists in the importance of the geometric intepretation:

"I must call to your attention the place in Gauss in which this foundation of complex numbers, by means of their geometric interpretation, is set out with full emphasis, since it was this which first exhibited the general importance of complex numbers. (...) For him, the right to operate with complex numbers is justified by the geometric interpretation which one gives to them and to the operations with them. Thus he takes by no means the formal standpoint". (Klein, 58)

MORE LINKS

Equiangular spiral

In an equiangular spiral the angle between the position vector and the tangent is constant.

Dilation and rotation in an equiangular spiral

Two transformations of an equiangular spiral with the same general efect.