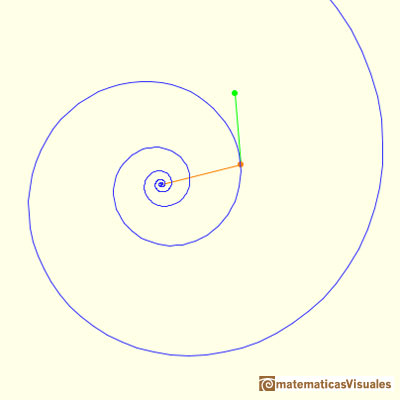
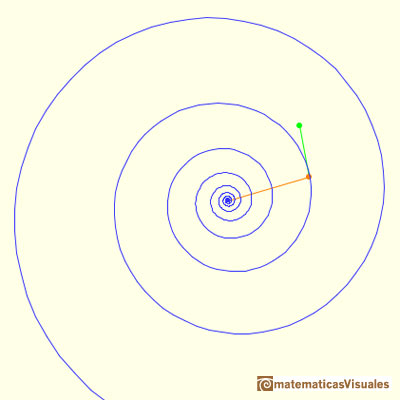
Equiangular Spiral. Rotation
Coxeter wrote about the Equiangular Spiral (Logarithmic Spiral):
"This curve was first recognized by Descartes. Jacob Bernouilli found it so fascinating that he arranged to have
it engraved on his tombstone with the inscription
Eadem mutata resurgo
These words (which E.T. Bell translates as "Though changed I shall arise the same") express a remarkable consequence of the way the curve
can be shifted along itself by a dilative rotation: any dilatation has the same effect on it as a rotation, and
vice versa." (Coxeter, p. 125)
Coxeter said that Steinhaus describes this property as an optical illusion: "If we turn the book about the vertex, the spiral
seems to grow larger or smaller. Two spirals having the same constant angle with the radii are congruent." (Steinhaus, p. 132). Steinhaus
wrote about the relation between Logarithmic Spirals and pursuing paths.
REFERENCES
Coxeter - Introduction to Geometry (John Whiley and sons)
Hugo Steinhaus, Mathematical Snapshots, Dover Publications (third edition, 1999)
D'Arcy Thompson - On Growth and Form. (Cambridge University Press)
MORE LINKS
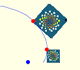
A Dilative Rotation is a combination of a rotation an a dilatation from the same point.
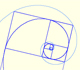
Two equiangular spirals contains all vertices of golden rectangles.
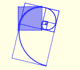
The golden spiral is a good approximation of an equiangular spiral.
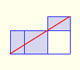
From Euclid's definition of the division of a segment into its extreme and mean ratio we introduce a property of golden rectangles and we deduce the equation and the value of the golden ratio.
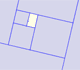
A golden rectangle is made of an square and another golden rectangle.
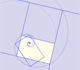
A golden rectangle is made of an square an another golden rectangle. These rectangles are related through an dilative rotation.

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
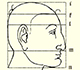
He studied transformations of images, for example, faces.

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.
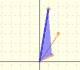
We can see it as a dilatative rotation.

 PREVIOUS
PREVIOUS

















 NEXT
NEXT








