The regular dodecahedron is a platonic polyhedron very well known from Antiquity.
Leonardo da Vinci drew two dodecahedra for Luca Pacioli's book 'The Divine Proportione'.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.
Albert Durer published a plane net of a dodecahedron for the first time in 1525.
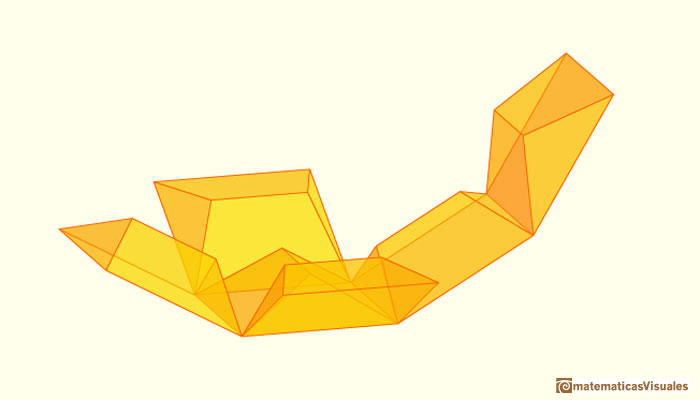
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
Kepler was interested in this wonderful geometric body (For example, you can see this drawing in his book
'Harmonices Mundi - The Harmony of the World', (1619)
(Read the original book at Posner Memorial Collection):
We have already studied a lot of properties of this beautiful polyhedron in matematicasVisuales:

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
And we know how to calculate its volume:

One eighth of a regular dodecahedon of edge 2 has the same volume as a dodecahedron of edge 1.
In this page we are going to study some relations between the dodecahedron and the cube.
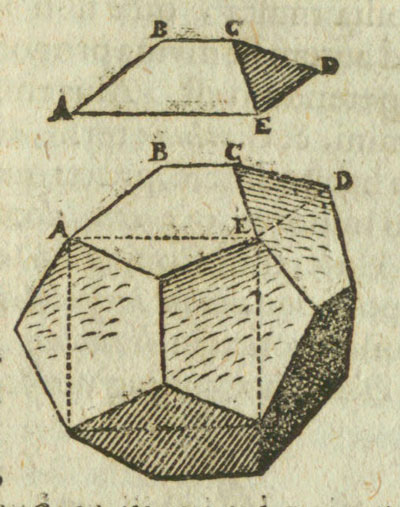
A cube can be inscribed in a dodecahedron so that each edge of the cube lies in a face of the dodecahedron and joins two alternate vertices
of that face. (Ball and Coxeter, p. 131)
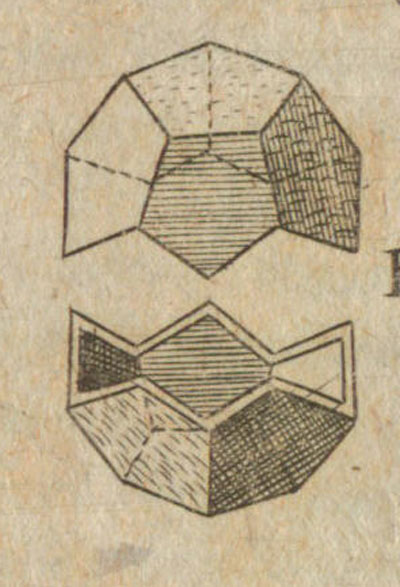
Kepler showed us this construction and saw the dodecahedron as a cube with six roofs added:
In the interactive application in this page you can see how a dodecahedron can be fold into a cube:




I encourage you to build your own polyhedron:
To calculate the volume of a dodecahedron of side length 1 you can remember some properties of the golden ratio:

The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.

One eighth of a regular dodecahedon of edge 2 has the same volume as a dodecahedron of edge 1.
The volume of a dodecahedron is the volume of a cube plus six times the volume of a roof.
The side length of the cube is equal to a diagonal of the pentagon, then:
Now we are going to calculate the volume of one roof.
One property of this roof is that its height is 1/2.
We can build a roof with Zome:
We can consider two parts of the roof:
Then the volume of one roof is:
And the volume of a dodecahedron of side lenght 1 is
Five cubes inside a dodecahedron:
REFERENCES
Hugo Steinhaus - 'Mathematical Snapshots' - Oxford University Press - Third Edition.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
 NEXT
NEXT

If you fold the six roofs of a regular dodecahedron into a cube there is an empty space. This space can be filled with an irregular dodecahedron composed of identical irregular pentagons (a kind of pyritohedron).
 PREVIOUS
PREVIOUS

The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
MORE LINKS

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.

One eighth of a regular dodecahedon of edge 2 has the same volume as a dodecahedron of edge 1.

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron

The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.
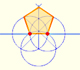
You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.
In his book 'Underweysung der Messung' Durer draw a non-regular pentagon with ruler and a fixed compass. It is a simple construction and a very good approximation of a regular pentagon.
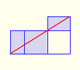
From Euclid's definition of the division of a segment into its extreme and mean ratio we introduce a property of golden rectangles and we deduce the equation and the value of the golden ratio.
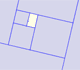
A golden rectangle is made of an square and another golden rectangle.
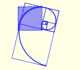
The golden spiral is a good approximation of an equiangular spiral.





























 NEXT
NEXT
 PREVIOUS
PREVIOUS























