
In the article Kepler: The Volume of a Wine Barrel published by MathDl (Loci, June 2010) I presented some interactive applications around the anecdote that lead to Kepler to study volumes of barrels and other bodies and to write his book (published in 1615) "Nova Stereometria doliorum vinariorum" (New solid geometry of wine barrels) where he used some infinitesimal techniques previous to the discovery of differential and integral calculus by Newton and Leibnitz.
Following Toeplitz's approach we presented some interesting calculations related to the anecdote.

Now we are going to see how Kepler stated one optimization problem and to study some calculations that Kepler really did to a better understanding of the problem.
You can see the whole book "Nova Stereometria doliorum vinariorum" in The Posner Library)

In this book, Kepler tried to calculate the volume of several bodies, in particular the volume of barrels. He intended to understand how its volume change in relation with its shape.
He simplified the problem and started to study simpler bodies like cylinders and prisms.
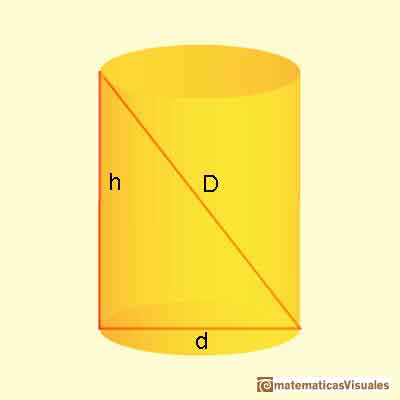
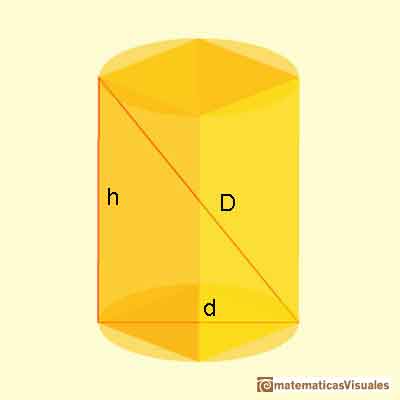
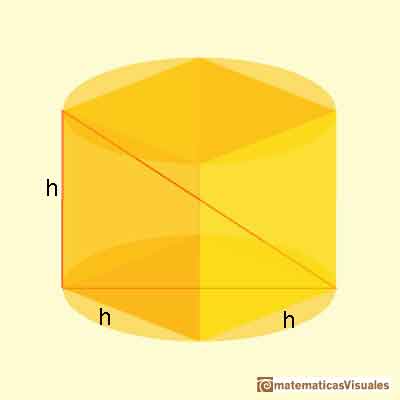
In this context he solved the following optimization problem: Given a diagonal D, which is the largest cylinder that has D as a diagonal? Which is the ratio between the base diameter and the height of such a cylinder?

Kepler tried to understand how the volume of a cylinder changes when we consider different heights.
Notice that, as D is fixed, all these cylinders are inscribed in a sphere with D as a diameter.
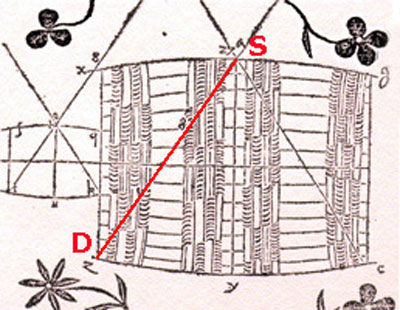
To a better understanding of the problem, Kepler studied a particular case and did some calculation ("Praxis"):
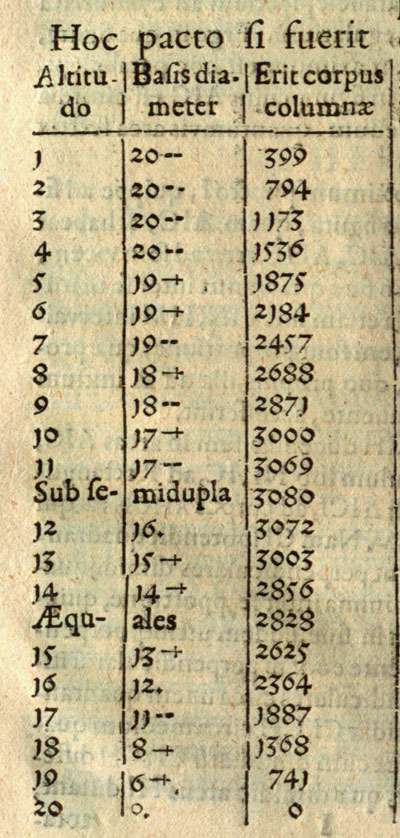
Here is the page where Kepler wrote his data:

and the table. This table has three columns, the first two are the height and the diameter of the base of the cylinder:
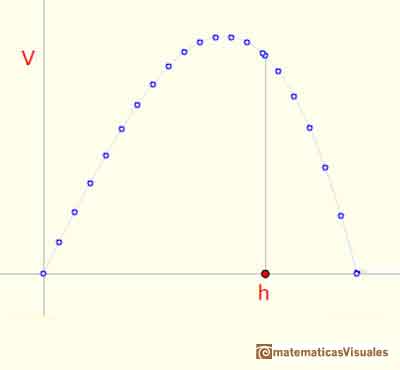
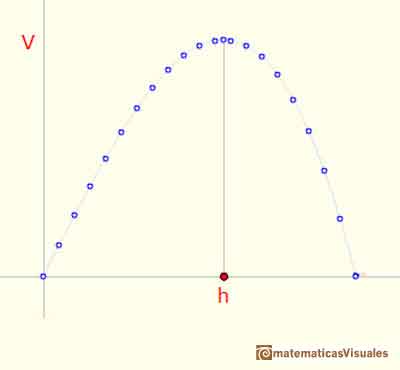
The video shows three parts: at the bottom right there is a cylinder with a prims inside, this is a geometric model that we can rotate. To the left there is the table with Kepler's data. We can see how changing the pointer we change the x-value in the graph that relates the height, h and the volume V. Kepler did not draw a graph but he was interested in studying how the volume changes as h changes.
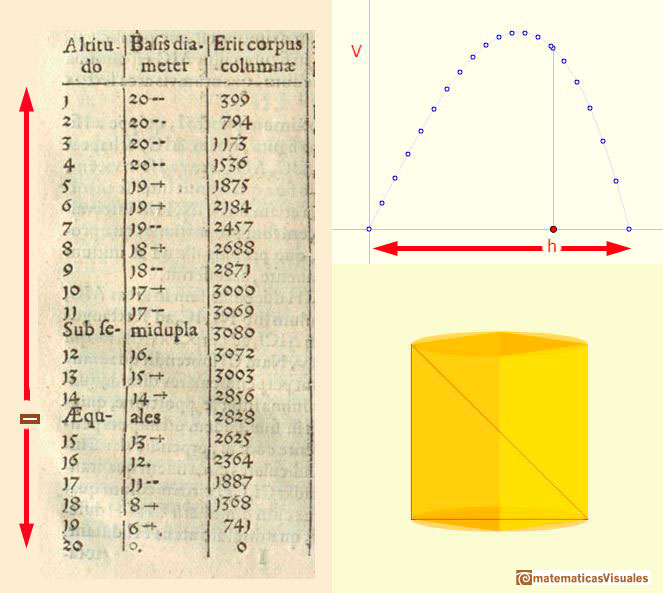
Looking at the graph it is easy to guess that there is a value of the height that gives us the maximum volume. It is very important to notice that around this maximum value the volume changes little.
Kepler was aware of that. These ideas were later developed by Fermat, Leibniz and Newton.
To understand the data that Kepler used we could start deducing the value of D in this case. For doing that we can see the extreme cases:
When h = 0:

And when h = 20:


Then the value of D is:
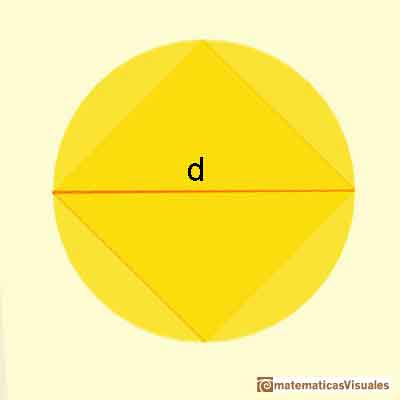
The second column is a calculation of the diameter of the cylinder (d) as the height changes. It is an application of the Pythagorean Theorem.

We can see that Kepler only approximate the result and put + or -. We are going to see later that the exact data is not really needed for his purpose, the calculation of volumes. But with our modern devices it is very easy to complete the table with more accuracy (but not exactness!) and to compare our table with Kepler's data (you can use a calculator or a spreadsheet):
Now we are going to see the third column. This column is about a volume but we understand very soon that these are not the volumes of cylinders because we know that the volume of a cylinder involves pi (with its infinite decimals) and the numbers that Kepler wrote are natural numbers. As Kepler wanted to study the variations of the volume of a cylinder and for what value of the height this volume reaches its maximum he can delete the pi factor or whatever factor he wanted because these proportional factors will not affect the conclusion. But there is a better reason, Kepler understood perfectly well that to study the problem of maximizing the volume of a cylinder inscribed in an sphere is enough to study a simpler case, to study the parallelepiped with square base inscribed in the sphere that maximizes the volume. This is a very usual process that mathematicians use to approach a problem, to study simpler cases, to reduce the problem to a simpler one. In our case, Kepler started to study barrels, then cylinders and now prisms.
Kepler used the latin word "column" to refers to this parallelepiped with square base. We can translate it by column, pillar or post. Following the english translation of Tikhomirov's book we are going to use the word "post".

We can now deduce the formula that Kepler used.
Remember that d is:
First, we can calculate the area of the base:
Now the volume of the post:
Kepler multiply this formula by two, to avoid dividing and because remember that the barrel was measured insertir a row from hole of the middle of the barrel.
See that we do not need the second column!
We can complete the table and compare it with Kepler's:
We can see that Kepler considere two special cases. One is between 14 and 15, with the word "Aequales". This is when the diameter of the base of the cilinder (the diagonal of the base square) is equal to its height:
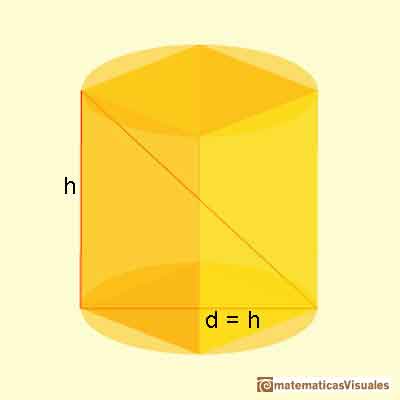
The value of h=d is
And the volume of the post when h=d is:

We can see that this case is not a maximum:
When the cilinder has its hight equal to its diameter the volume is not a maximum:

The second special value is between 11 and 12 and Kepler wrote "Sub semidupla".
This case is the maximum volume. The prism is a cube.
We can use the Pythagorean Theorem again and write:
The height in this case is:
And the volume is:
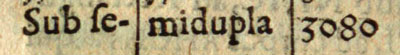
This is the maximum (it has to be probed!)

After this "praxis" Kepler stated this maximum problem as Theorem IV of part two:

Theorem IV. Of all rectangles parallelepipeds with a square base inscribed in a sphere the one with largest volume is the cube.
You can see Kepler's geometric demonstration in Tikhomirov's book (pp. 50-53).
One of the key result in this book is Theorem V of part two:

"Of all cylinders with the same diagonal, the largest and most capacious is that in which the ratio of the base diameter to the height is the square root of two". (From Tikhomirov's book English translation)
Kepler used the word "semidupla". We can calculate d in this case, and we can guess that this is the meaning of the word "semidupla":
This theorem provides the solution of the following problem: Inscribe in a given sphere a cylinder of maximal volume.
But this is simple with Theorem IV because the volume of a cylinder is:
It is to say:
Then the volume of the more capacious cylinder has inscribed a cube that is the more capacious post.
After proving this theorem Kepler wrote:

"From this is clear that, when making a barrel, Austrian barrelmakers, as if guided by common and geometric sense, take as the radius of a bottom a third of the lenght of a stave. When this is done, the cylinder constructed in the mind between two bottoms will consist of two halves, each of which will be close to the conditions of theorem V and will thus have maximal capacity even if one deviated somewhat from the exact rules during the making of the barrel, because figures closed to the optimal change their capacity very little ... This is so because near a maximum the decrements on both sides are in the beginning only imperceptible." (Kepler, translated by Tikhomirov)
"Kepler's concluding words contain the fundamental algorithm for finding extrema that was later shaped into an exact theorem. First described (for polynomials) by Fermat (1629) and then, in general form, by Newton and Leibniz, this algorithm was later called 'Fermat's theorem.'" (Tikhomirov)
REFERENCES
MORE LINKS

















 NEXT
NEXT

 PREVIOUS
PREVIOUS

