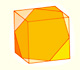
Construir y tocar modelos de octaedro es una experiencia más interesante de lo que parece a primera vista.
Podemos usar cartulina y partir del desarrollo del octaedro (formado por ocho triángulos equiláteros):
También lo podemos hacer con papiroflexia (construcción muy básica de origami modular). Esta construcción nos muestra que
los seis vértices de este poliedro están en tres cuadrados que se encuentran en tres planos ortogonales:
Podemos usar doce tubos de plástico o aluminio:
Una figura de origami modular sencilla e instructiva está formada por los tres cuadrados en planos ortogonales
dos a dos que contienen las 12 aristas y los 6 vértices del
octaedro regular.
Su construcción es simple y aquí podemos ver cómo se hace:
El objetivo es, además, construir una cubo para poder poner dentro el octaedro que hemos hecho con papiroflexia.
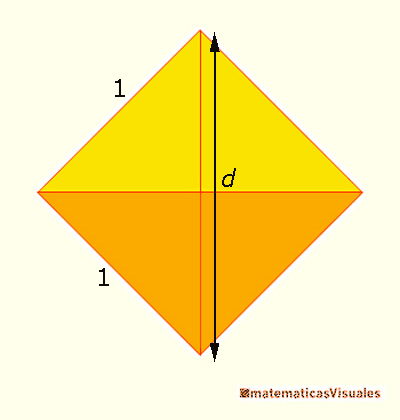
Manipulando un octaedro enseguida vemos que está formado por dos pirámides de base cuadrada.
También vemos que la altura de estas dos pirámides es una diagonal de un cuadrado.
La diagonal de un cuadrado de lado 1 es:
Por lo tanto, el volumen de un octaedro de lado 1 es (la fórmula del volumen de una pirámide es un tercio del área de la base por la altura):
El volumen de un octaedro de arista a es:
Esta página contiene una animación interactiva desarrollada en Flash.
Si no puedes verla, en el siguiente enlace puedes ver un vídeo sobre ella:

Añadiendo cuatro tetraedros a un octaedro podemos obtener un tetraedro. Calculamos el volumen de un tetraedro a partir del volumen de un octaedro y usando semejanza.
Podemos calcular ahora el volumen de un tetraedro.
Empezamos considerando un tetraedro de arista 2:
Podemos escribir la relación (volumen de figuras semejantes):
Un tetraedro de arista 2 está formado por un octaedro y cuatro tetraedros de arista 1:
Por lo tanto, el volumen de un octaedro es cuatro veces el volumen de un tetraedro y podemos recalcular el
volumen de un tetraedro.
REFERENCIAS
Hugo Steinhaus, Instantáneas matemáticas (pags. 187-192),Editorial Salvat (1986)
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
MÁS ENLACES

Añadiendo cuatro tetraedros a un octaedro podemos obtener un tetraedro. Calculamos el volumen de un tetraedro a partir del volumen de un octaedro y usando semejanza.
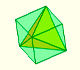
Podemos inscribir un tetraedro en un cubo. A partir de esta construcción calculamos el volumen de un tetraedro.

El cálculo del volumen de un octaedro es sencillo aplicando el teorema de Pitágoras y considerando que el octaedro está formado por dos pirámides.

El primer dibujo del desarrollo plano del octaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Demostración dinámica e interactiva del teorema de Pitágoras, inspirada en la de Euclides.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
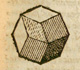
Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.
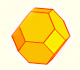
El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.

Podemos dibujar los desarrollos planos en cartulina y construir poliedros uniendo solapas con pegamento.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.

Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.

El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.

Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.

Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro estrellado (que Kepler llamó stella octangula).

Kepler usó una aproximación infinitesimal intuitiva para calcular el área de un círculo.
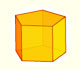
Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.

Los cilindros son superficies de revolución que pueden desarrollarse en un plano. Se explica cómo calcular la superficie lateral y total de un cilindro.
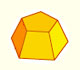
Desarrollos planos de pirámides y de troncos de pirámide de base regular con diferentes números de lados.

Desarrollos planos de conos y troncos de cono. Cálculo del área lateral de estas figuras.
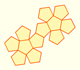
El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
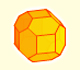
Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.

















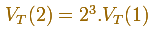


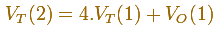


 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR