matematicasVisuales |Complejos

Complejos


			$Multifunciones: Potencias con exponente fraccionario \| matematicasVisuales$

Multiplicación de complejos
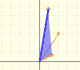	Multiplicando dos números complejos Se puede ver como una rotación dilatativa.
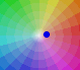	La multiplicación como una transformación del plano complejo Geométricamente, la multiplicación por un complejo es una transformación del plano que consiste en una rotación y una expansión o contracción (rotación dilatativa).
	Progresión geométrica compleja Una progresión geométrica compleja está relacionada con las espirales equiangulares.
Funciones complejas
	Funciones polinómicas complejas (1): Potencias de exponente natural Las potencias de exponente natural tienen un cero de multiplicidad n.
	Funciones polinómicas complejas (2): Polinomio de grado 2 Un polinomio de grado 2 tiene dos raíces o ceros. En esta representación podemos ver los óvalos de Cassini y la lemniscata.
	Funciones polinómicas complejas (3): Polinomio de grado 3 Un polinomio de grado 3 tiene tres ceros o raíces. Podemos modificar los tres ceros de este tipo de polinomios.
	Funciones polinómicas complejas (4): Polinomio de grado n Un polinomio de grado n tiene n ceros o raíces.
	Funciones polinómicas complejas (5): Polinomio de grado n (variante) Podemos controlar qué partes del plano complejo se muestran con colores.
	Cero y polo Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.
	Cero y polo (variante) Tenemos más control sobre qué partes del plano complejo se representa con colores.
	Transformaciones de Moebius Una primera aproximación a estas transformaciones. Representación de dos haces coaxiales de circunferencias ortogonales.
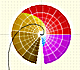	Función exponencial compleja La función exponencial compleja extiende la función exponencial real al plano complejo.
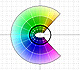	La función coseno compleja La función coseno compleja extiende la función real al plano complejo. Es una función periódica que comparte varias propiedades con la función real.
	La función coseno compleja: transformación de una recta horizontal La función coseno compleja transforma rectas horizontales en elipses cofocales.
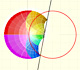	Inversión La inversión es una transformación del plano que transforma rectas y circunferencias en rectas y circunferencias.
	Inversion: una transformación anticonforme La inversión preserva la magnitud de los ángulos pero invierte el sentido. Circunferencias ortogonales se transforman en circunferencias ortogonales
$Multifunciones: Potencias con exponente fraccionario \| matematicasVisuales$	Multifunciones: Potencias con exponente fraccionario El concepto de función puede extenderse permitiendo que f(z) tenga diferentes valores para un valor z. En este caso decimos que f es una función multivaluada o multifunción.
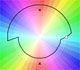	Multifunciones: Dos puntos de ramificación Una multifunción puede tener más de un punto de ramificación. La multifunción considerada en esta página tiene dos valores y dos puntos de ramificación.
Polinomios de Taylor
	Polinomios de Taylor: función racional compleja con 2 singularidades Podemos estudiar la aproximación a esta función por el polinomio de Taylor y su convergencia en el círculo de convergencia.
	Polinomios de Taylor: función exponencial compleja La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.
	Polinomios de Taylor: función coseno compleja La función coseno compleja tiene un desarrollo de Taylor que converge en todo el plano complejo.