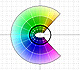
Vamos a estudiar la función compleja
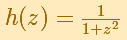
Nos ayudará a comprender el comportamiento de la serie de Taylor de una función real que no tiene singularidades reales. Esta función real coincide con la función compleja en el eje real:
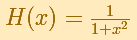
La función real no tiene singularidades pero en el plano complejo tiene dos singularidades, en z = i y en z = -i.

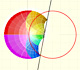
Si consideramos la serie de potencias compleja centrada en algún punto, existe un círculo centrado en ese punto tal que la serie converge en todos los puntos del interior del círculo y diverge fuera de ese círculo. Vamos a ver que el radio de convergencia es la distancia desde el centro a la singularidad más próxima.
Es muy importante el hecho de que si la serie de potencias converge en un punto, entonces su valor puede aproximarse por una suma parcial (polinomio), y considerando un grado suficientemente grande podemos hacer la aproximación tan precisa como queramos. (Tristan Needham)
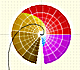
Por ejemplo, esta es la representación del polinomio de Taylor de grado 6:

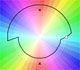
El Resto es la diferencia entre la función y el polinomio. Un color claro, casi blanco, indica que el módulo es pequeño. Conforme incrementamos el grado del polinomio el área blanca se aproxima al círculo de convergencia.
Esta es una representación del resto cuando consideramos el polinomio de Taylor de grado 6. La aproximación es muy precisa cerca del centro:

La aproximación es mejor cuando consideramos el polinomio de grado 50:


Si restringimos nuestra visión al círculo de convergencia podemos ver cómo estos polinomios aproximan la función dentro del círculo de convergencia.
Esta es una representación del polinomio de Taylor de grado 50 sólo dentro del círculo de convergencia:

Y esta es una representación de la función restringida al mismo círculo. Podemos ver que la imagen de arriba es semejante a esta.

Otro ejemplo, cuando el polinomio de Taylor tiene sólo grado 15:
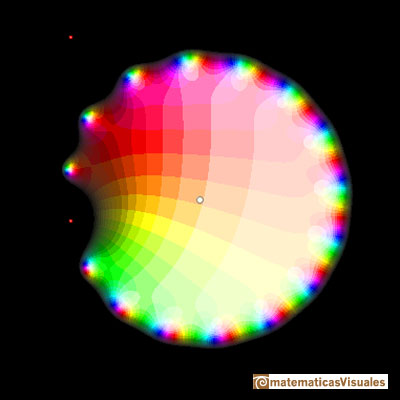
El mismo polinomio pero restringido al interior del círculo de convergencia:

Y la función restringida al mismo círculo:
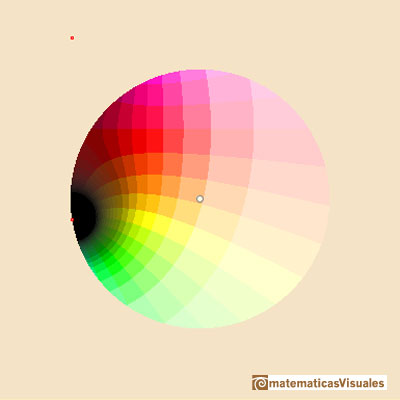
Dentro del círculo de convergencia la función y la aproximación son semejante pero fuera pueden ser muy diferentes.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES