Ya hemos visto el rombicuboctaedro en una aplicación interactiva inspirada en los dibujos de Leonardo da Vinci. Es un sólido arquimediano
formado por 8 triángulos y 12+6 cuadrados.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro.
El poliedro que estudiamos en esta página es muy parecido al rombicuboctaedro pero es menos simétrico. En general, no se considera que sea uno
de los sólidos arquimedianos.
El pseudo rombicuboctaedro ha sido redescubierto muchas veces. Así describen Ball y Coxeter el descubrimiento del poliedro por Miller:
"Cuando intentaba hacer un modelo de este poliedro [el rombicuboctaedro], J.C.P. Miller
descubrió accidentalmente un 'pseudo-rombicuboctaedro' formado igualmente por 8 triángulos y 18 cuadrados, e isogonal en un sentido
relajado o 'local' (cada vértice está rodeado por un triángulo y tres cuadrados), pero no en un sentido estricto (que implica que
la apariencia del sólido como un todo debe permanecer el mismo cuando lo miramos desde la dirección de cada uno de sus vértices."
(Ball y Coxeter, p. 137)
El pseudo rombicuboctaedro es uno de los sólidos de Johnson.
"Ha sido llamado de varias maneras: pseudo-rombi-cub-octaedro, sólido de Miller y girobicúpula cuadrada elongada.
Este último nombre proviene de Johnson e indica cómo se construye el poliedro a partir de poliedros elementales:
tomamos dos cúpulas (bicúpula cuadrada), las rotamos relativamente una respecto de otra (giro) y las separamos por
un prisma (elongación)." (Cromwell, p.89)
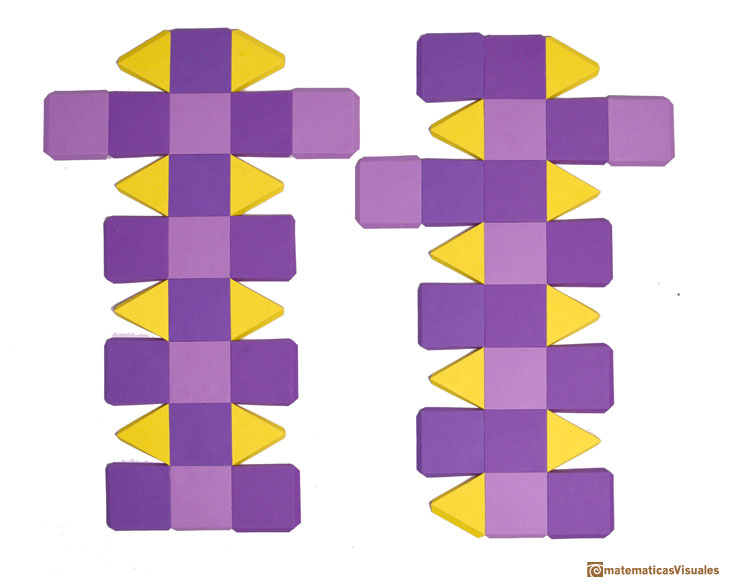
Aunque estos dos poliedros tienen las mismas caras no pueden construirse a partir de la misma red.
Es sencillo hacer estos dos poliedros con cartulina. Se pueden descargar plantillas con triángulos y cuadrados en el siguiente enlace.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.
El rombicuboctaedro está a la izquierda y el pseudo rombicuboctaedro a la derecha.
Cuando veamos el dibujo que Leonardo da Vinci hizo del rombicuboctaedro aumentado para 'La Divina Proporción' de Luca Pacioli surgirá la duda de si Leonardo se basó
en un rombicuboctaedro o en un pseudo rhombicuboctaedro para realizar la ilustración. Quizás fue un pequeño error, una curiosidad que estudiamos en la siguiente
página.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro aumentado.
REFERENCIAS
W.W.W. Rouse Ball and H.S.M. Coxeter, 'Mathematical Recreations & Essays', The Macmillan Company, New York, 1947.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999. (pp. 89 and 366-369)
MÁS ENLACES

En esta segunda versión del rombicuboctaedro aumentado podemos separar las pirámides y ver el interior de la figura. Luca Pacioli escribió que 'podemos ver el interior solo con nuestra imaginación'. La aplicación interactiva solo nos ayuda a ello.

A partir de un rombicuboctaedro podemos añadir pirámides a sus caras. Obtenemos un precioso poliedro que parece una estrella.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro estrellado (que Kepler llamó stella octangula).

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación del poliedro de 72 caras (Septuaginta) también conocido como esfera de Campanus de Novara.

El primer dibujo del desarrollo plano del octaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.
El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.
Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.














 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
































