Esta página es complementaria de la exposición: "Los sólidos arquimedianos" que se realiza en el IES Alonso
Quijano de Alcalá de Henares durante el mes de junio de 2022.
Diseño: Miguel Cardil.
Es la tercera exposición sobre poliedros que se realiza en el IES Alonso Quijano durante estos últimos años. Las otras dos fueron
'Homenaje a Kepler: las abejas y el dodecaedro rómbico' (2020) y
'Los sólidos platónicos' (2021).
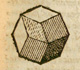
Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

Exposición sobre los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro. Construcción de los poliedros encajados. El Omnipoliedro. Algunas propiedades básicas que se pueden aprender de esta construcción.
Los poliedros arquimedianos son poliedros convexos cuyas caras son polígonos regulares de más de un tipo. Se combinan dos o más tipos de
polígonos para formar estos poliedros.Diciéndolo de un modo sencillo, también debemos exigir que los vértices de cada uno de estos poliedros 'sean iguales'
Fueron descubiertos por Arquímedes pero no ha quedado rastro de su trabajo sobre estos poliedros. Hay una referencia del matemático Pappus
en la que afirma que Arquímedes descubrió los trece poliedros que llevan su nombre. Posteriormente, Kepler redescubre estos poliedros.
La mayoría de los poliedros expuestos han sido recortados y montados por alumnos de 1º ESO del IES Alonso Quijano. Tienen unos
doce años y han realizado un trabajo muy bueno. Hecho entre todos, por equipos y trabajando un poco en casa, ha sido realizado
con gusto por los alumnos.
La técnica utilizada ha sido recortar polígonos regulares en cartulina y unir las caras con gomas elásticas.
En el siguiente enlace se hace una descripción más detallada de este material, su origen y difusión, plantillas para descargar y ejemplos:

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.
Objetivos
Con la construcción de estos poliedros arquimedianos y su exposición solo se ha pretendido disfrutar de su belleza y hacer una presentación
muy sencilla.
Comprender que hay una relación entre estos sólidos arquimedianos y los platónicos. Los cinco sólidos platónicos están emparejados (dualidad),
de modo que el cubo y el octaedro son poliedros duales, el icosaedro y el dodecaedro forman otra pareja y el tetraedro es autodual. Mostramos
que los sólidos arquimedianos puede considerarse que forman tres familias: la relacionada con el tetraedro, la relacionada con el cubo y octaedro
y la relacionada con el icosaedro y dodecaedro.
Vemos que algunos de estos poliedros arquimedianos se obtienen cortando los vértices de correspondientes sólidos platónicos.
Este procedimiento se llama truncamiento. Pero no todos los poliedros arquimedianos se obtienen por truncamiento de algún
sólido platónico.
Información preliminar
Como una introducción podría ser conveniente repasar la familia de poliedros regulares (los sólidos platónicos) y la idea de emparejamiento
entre esos sólidos (dualidad):

Presentación de los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro.

Estudiamos el concepto de dualidad de poliedros aplicado a los sólidos platónicos. El cubo y el octaedro son duales, el icosaedro y el dodecaedro son duales y el tetraedro decimos que es autodual.
A) La familia del tetraedro
A.1) Tetraedro truncado
Obtenemos un sólidos arquimediano truncando convenientemente los cuatro vértices de un tetraedro. El poliedro se llama tetraedro truncado.
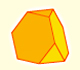
El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su tetraedro truncado.
B) La familia del cubo-octaedro
B.1) Cubo truncado
Truncando un cubo obtenemos un cubo truncado.
Éste es el desarrollo plano del cubo truncado:
B.2) Octaedro truncado
Truncando un octaedro obtenemos un octaedro truncado.
Este poliedro es muy interesante pues tesela el espacio.

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.
B.3) Cuboctaedro
Si truncamos un cubo (o un octaedro) 'con más profundidad' hasta el centro de sus aristas obtenemos, en ambos casos, el mismo poliedro que se llama
cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices
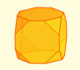
Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.
El cuboctaedro y el dodecaedro rómbico son poliedros duales.
El dodecaedro rómbico es un poliedro descubierto por Kepler y que tiene muy interesantes propiedades, entre ellas, que está
relacionado con cómo las abejas construyen sus panales y que tesela el espacio.

La Humanidad ha estdo siempre fascinada por cómo las abejas construyen sus panales. Kepler relacionó la forma de los panales con un poliedro que llamamos dodecaedro rómbico.
B.4) Pequeño rombicuboctaedro
También están relacionados con el cubo y el octaedro dos poliedros que llevan el prefijo 'rombi'.
El primero es el rombicuboctaedro (o pequeño rombicuboctaedro)

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro.
Es interesante destacar que hay una variante de este poliedro que, en algunas ocasiones, también se considera un poliedro de
Arquímedes. Es el llamado pseudo-rombicuboctaedro. Si consideraramos este caso, entonces habría catorce sólidos arquimedianos.

También llamado girobicúpula cuadrada elongada. Es muy parecido al rombicuboctaedro pero es menos simétrico.
B.5) Gran rombicuboctaedro
El otro se llama gran rombicuboctaedro.
El prefijo 'rombi' se debe a que alguna de las caras de estos poliedros son coplanares con las del cubo y las del octaedro. Pero otras doce
las comparte con un poliedro rómbico que se llama dodecaedro rómbico.

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.
B.6) Cubo romo
Un sexto poliedro de esta familia es especialmente curioso. Se llama cubo romo. Se puede construir con dos orientaciones distintas y
resultan dos poliedros simétricos (a este tipo de parejas de formas especulares se las llama enantiomorfas o quirales).
C) La familia del icosaedro-dodecaedro
C.1) Icosaedro truncado
Es un poliedro muy interesante pues está relacionado con la estructura molecular del Carbono-60. También recibe el nombre de
Fullereno y está presente en muchos campos de fútbol pues éste es un poliedro que se usa para construir los balones de muchos deportes.
C.2) Dodecaedro truncado
C.3) Icosidodecaedro
Truncando un dodecaedro (o un icosaedro) hasta el centro de cada una de sus aristas se obtiene el icosidodecaedro.
El icosidodecaedro y el poliedro rómbico triacontaedro son poliedros duales.
C.4) Pequeño rombicosidodecaedro
Los poliedros de la familia del icosaedro-dodecaedro con el prefijo 'rombi' tienen caras en los planos del dodecaedro, del icosaedro y
del triacontaedro (estas son los treinta cuadrados).
C.5) Gran rombicosidodecaedro
C.6) Dodecaedro romo
Precioso poliedro que, al igual que el cubo romo, tiene dos formas enantiomorfas.
MÁS ENLACES

El diseñador italiano Bruno Munari pensó 'Acona Biconbi' como un trabajo de escultura. También es un juego de construcción con el que podemos jugar con colores y formas.

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

Podemos dibujar los desarrollos planos en cartulina y construir poliedros uniendo solapas con pegamento.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.

Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.

El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.

Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.

Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.

Material para la sesión del TTM (Zaragoza, el 10 de marzo de 2023). Con plantillas para descargar y construir varias figuras geométricas.

Material para la sesión del TTM (Zaragoza, el 20 de Octubre de 2017). El objetivo principal es disfrutar con las Matemáticas y fomentar la construcción de poliedros por su valor estético y también porque nos facilitan la comprensión de resultados matemáticos.

Material para la sesión del TTM (Zaragoza, el 19 de Octubre de 2018). Diferentes construcciones del icosaedro nos ayudan a comprender sus propiedades. El objetivo principal es disfrutan construyendo poliedros.

Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su tetraedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.

El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.

Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.









































 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR







































